Cosimo scrive: Esercizio triangolo rettangolo

Pubblicato il da Lo StaffLascia un commento
0

Uno studente scrive

Corpo del messaggio:
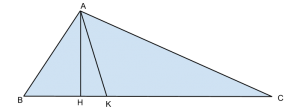
1) In un trangolo rettangolo ABC, di cateti 3a e 4a, traccia l’ altezza AH relativa all’ ipotenusa BC e la bisettrice AK dell’ angolo retto. Calcola l’ area del triangolo AKH.

 

 

Risposta dello staff

triangolorettangolo (1)

 

Imponiamo che:

AB=3a

AC=4a

Ricaviamo subito con il teorema di Pitagora BC:

BC= \sqrt {AB^2+AC^2}=\sqrt {9a^2+16a^2}=\sqrt {25a^2}=5a

Ricaviamo anche BH col teorema di Euclide:

BH=\frac {AB^2}{BC}=\frac {9a^2}{5a}=\frac 95 a

Quindi troviamo AH col teorema di Euclide sapendo che:

HC=BC-BH=5a-\frac 95a= \frac {16}{5}a

AH= \sqrt {BH \cdot HC}= \sqrt{\frac {9}{5}a \cdot \frac {16}{5}a}=\frac {12}{5}a

Visto che AK è bisettrice sfruttiamo la proprietà:

AB:AC=BK:KC

Poniamo BK=x e quindi CK=5a-x

\frac {3a}{4a}= \frac {x}{5a-x}

\frac 34 =\frac {x}{5a-x}

15a-3x=4x

7x=15a

x=\frac {15}{7}a

Ora che sappiamo BK e BH, calcoliamo HK così da poter avere l’area:

HK=BK-BH=\frac {15}{7}a - \frac {9}{5}a= \frac {75-63}{35}a=\frac {12}{35}a

L’area quindi sarà:

A_{AHK}= \frac {HK \cdot AH}{2}=\frac {\frac {12}{35}a \cdot \frac {12}{5}a}{2}=\frac {72}{175}a^2

 

(Questa pagina è stata visualizzata da 181 persone)

Lascia un commento