Luca scrive: problema bisettrice triangolo rettangolo

Pubblicato il da Lo StaffLascia un commento
0

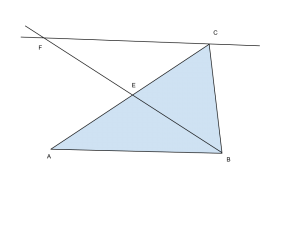
Uno studente scrive:

Nel triangolo ABCD si ha: AB=20cm, AC=18cm, BC=12cm. Traccia la bisettrice dell’ angolo B ed indica con E il suo punto di intersezione con AC. Conduci dal vertica C la parallela ad AB, che interseca il prolungamento dell bisettrice BE nel punto F. Calcola CF, AE, EC.

 

Risposta dello staff

triangolobisettrice

 

Sapendo che BE è la bisettrice possiamo subito sfruttare la proprietà che ci dice:

AB:BC=AE:EC

Ora, ponendo AE=x, avremo che EC=18-x

e quindi, sostituendo otterremo:

\frac {20}{12}=\frac {x}{18-x}

\frac {5}{3}=\frac {x}{18-x}

90-5x=3x

8x=90

x=\frac {45}{4} \mbox { cm}.

Quindi:

AE=\frac {45}{4} \mbox { cm}

CE=(18-\frac {45}{4}) \mbox { cm}=\frac {27}{4} \mbox { cm}

Per trovare la lunghezza di CF, basterà notare che ABE e EFC sono simili e quindi:

CF:AB=EC:AE

CF=\frac {\frac {27}{4} \cdot 20}{\frac {45}{4}} \mbox { cm}= 12 \mbox { cm}

 

 

 

(Questa pagina è stata visualizzata da 181 persone)

Lascia un commento