Eleonora scrive: Esercizi disequazioni fratte

Pubblicato il da Lo StaffLascia un commento
0

Corpo del messaggio:
Salve,avrei bisogno di una mano per risolvere questi esercizi.Grazie in anticipo.
Disequazioni fratte numeriche :
(x-4)*(x+2)
__________ ≥0
x*(x^2+1)

(1-x)^4*(x-2)^3
_______________ >0
x*(x-3)^2

x +  7x+4
___  ______  <0

x-3 (x-3)^2

 

Analizziamo caso per caso:

    \[\frac {(x-4)(x+2)}{x(x^2+1)} \geq0\]

  • x-4 \geq 0 \iff x \geq 4
  • x+2 \geq 0 \iff x \geq -2
  • x >0
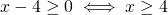
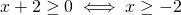
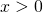
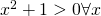  • x^2+1 >0 \forall x perchè somma di due quadrati.

Facendo il grafico otteniamo che la disequazione è verificata per:

-2 \leq x <0 \quad \lor \quad x \geq 4

 

Analizziamo caso per caso:

    \[\frac {(1-x)^4(x-2)^3}{x(x-3)^2} >0\]

  • (1-x)^4 > 0 \iff x \neq 1
  • (x-2)^2 > 0 \iff x > 2
  • x >0
  • (x-3)^2 >0 \iff x \neq 3.

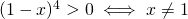
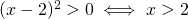
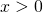
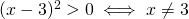Facendo il grafico otteniamo che la disequazione è verificata per:

x <0 \quad \lor \quad x > 2 \mbox { con } x \neq 3

 

Analizziamo caso per caso:

    \[\frac {x}{x-3} + \frac {7x+4}{(x-3)^2}<0\]

    \[ \frac {x^2-3x+7x+4}{(x-3)^2}<0\]

    \[ \frac {x^2+4x+4}{(x-3)^2}<0\]

    \[ \frac {(x+2)^2}{(x-3)^2}<0\]

    \[ \left(\frac {x+2}{x-3}\right)^2<0.\]

Essendo un quadrato per definizione questa non potrà mai essere verificata.

 

 

 

(Questa pagina è stata visualizzata da 140 persone)

Lascia un commento