Luca scrive: Esercizio sistema semplice

Oggetto: Sistema semplice (trigonometria)

Corpo del messaggio:
Buonasera,

sarei grato se riusciste a risolvere il numero 510 (in foto).

Vi ringrazio,
Luca.

$\begin{cases} x+y=\pi \\ 2senx+2cosy=\sqrt 3 +1 \end{cases}$

$\begin{cases} x=\pi-y \\ 2sen(\pi-y)+2cosy=\sqrt 3 +1 \end{cases}$

$\begin{cases} x=\pi-y \\ 2(seny+cosy)=\sqrt 3 +1 \end{cases}$

$\begin{cases} x=\pi-y \\ seny+cosy=\frac {\sqrt 3 +1}{2} \end{cases}$

$\begin{cases} x=\pi-y \\ seny+cosy=\frac {\sqrt 3 }{2}+\frac {1 }{2} \end{cases}$

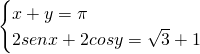
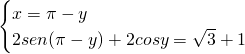
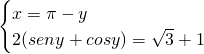
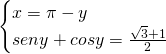
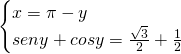
Senza bisogno di fare grossi calcoli ci accorgiamo che la somma della seconda equazione riguarda proprio angoli noti, quindi:

$y=\frac 16 \pi + 2k\pi \quad \lor \quad y=\frac 13 \pi + 2k\pi$

e da qui ricaviamo pure l’altra incognita:

$y=\frac 16 \pi + 2k\pi \quad \wedge \quad x=\frac 56 \pi -2k\pi$

$y=\frac 13 \pi + 2k\pi \quad \wedge \quad x=\frac 23 \pi -2k\pi$

(Questa pagina è stata visualizzata da 108 persone)

Matebook