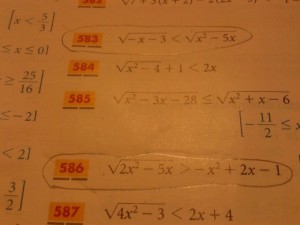Oggetto:

Corpo del messaggio:

 

 

Qui basterà osservare che:

Essendo un quadrato di binomio sempre positivo, e quindi, con il segno – davanti, sempre negativo, basterà studiare la positività del radicando per ottenere la soluzione della disequazione.

 

da cui:

.

 

N.B. Se una soluzione del radicando fosse stata sarebbe stata da escludere perchè avrebbe annullato anche il secondo fattore, rendendo non vera la disuguaglianza.

 

 

(Questa pagina è stata visualizzata da 96 persone)