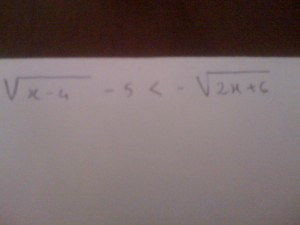Claudio scrive: Esercizio disequazione

Oggetto:

Corpo del messaggio:

$\sqrt{x-4} - 5 < - \sqrt {2x+6}$

Isoliamo le radici:

$\sqrt {x-4}+\sqrt{2x+6}<5$

Eleviamo al quadrato ricordando che le radici devono essere positive per costruzione:

$\begin{cases} x-4+2x+6+2\sqrt {(x-4)(2x+6)}<25 \\ x-4 \geq 0 \\ 2x+6 \geq 0 \end{cases}$

$\begin{cases} 3x+2+2\sqrt {(x-4)(2x+6)}<25 \\ x \geq 4 \\ x \geq -3 \end{cases}$

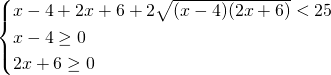
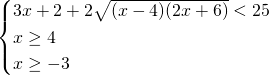
Possiamo eliminare la terza disequazione perchè inutile ai fini dei calcoli:

$\begin{cases} 2\sqrt {(x-4)(2x+6)}<23-3x \\ x \geq 4 \end{cases}$

$\begin{cases} 4(2x^2+6x-8x-24)<(23-3x)^2 \\ x \geq 4 \end{cases}$

$\begin{cases}8x^2+24x-32x-96<529-138x+9x^2 \\ x \geq 4\end{cases}$

$\begin{cases} x^2-130x+625>0 \\ x \geq 4 \end {cases}$

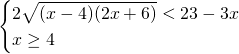
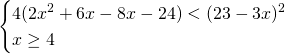
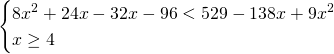
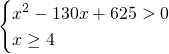
Analizziamo solo la disequazione e notiamo che:

$x^2-130+625=(x-5)(x-125)$ .

Quindi la disequazione è verificata per

$x<5 \quad \lor \quad x>125$

Il sistema nel complesso è verificato per:

$4 \leq x <5 \quad \lor \quad x>125.$

(Questa pagina è stata visualizzata da 107 persone)

Matebook