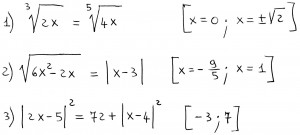Leandro scrive: Equazione irrazionale

Pubblicato il 2 Gennaio 2014 da Lo StaffLascia un commento

Oggetto: Equazione irrazionale ed equazione con moduli

Corpo del messaggio:

Come al solito, farei tre esercizi diversi:

$\sqrt[3]{2x}=\sqrt[5]{4x}$

Essendo radici di ordine diverso, eleviamo entrambe per il minimo comune multiplo degli indici stessi, ovvero eleviamo alla quindicesima:

$(2x)^5=(4x)^3$

$32x^5-64x^3=0$

$x^3(x^2-2)=0$

Da cui avremo:

$x^3=0 \Rightarrow x=0$

$x^2=2 \Rightarrow x= \pm\sqrt 2$ .

$\sqrt{6x^2-2x}=\left|x-3 \right|$

La condizione di esistenza $6x^2-2x \geq 0$ , sarà verificata per:

$x \leq 0 \quad \lor \quad x \geq \frac 13$

.

E’ inutile studiare la positività del valore assoluto, in quanto, questo sarà per definizione sempre positivo.

Eleviamo subito al quadrato e otteniamo:

$6x^2-2x=x^2-6x+9$

$5x^2+4x-9=0$

$x_{\frac 12}=\frac {-4 \pm \sqrt {16+180}}{10}= \frac {-4 \pm 14}{10}$

Da cui:

$x_1=-\frac 95$

$x_2=1$ .

Le soluzioni sono entrambe accettabili.

$\left|2x-5\right|^2=72+\left|x-4\right|^2$

Essendo i due valori assoluti elevati al quadrato, risulta inutile studiare la loro positività, tanto i termini positivi e negativi rimangono identici in ogni caso.

$4x^2-20x+25=72+x^2-8x+16$

$3x^2-12x+63=0$

$x^2-4x-21=0$

$(x+3)(x-7)=0$

$x_1=-3$

$x_2=7$

(Questa pagina è stata visualizzata da 70 persone)

Lascia un commento Annulla risposta

Devi essere connesso per inviare un commento.