Vincenzo scrive: Verifica di Matematica

Pubblicato il da Lo StaffLascia un commento
-1

Oggetto:

Corpo del messaggio:

IMG-20140108-WA0002

 

 

1) y=2x^2+x-1

Calcoliamo quello che ci serve:

V\left( -\frac {b}{2a}; -\frac {\Delta}{4a}\right) \rightarrow V \left( -\frac 14 ; -\frac {9}{8}\right)

F\left( -\frac {b}{2a};\frac {1-\Delta}{4a}\right) \rightarrow F \left( -\frac 14 ; -1\right)

Asse di simmetria: x=-\frac {b}{2a} \rightarrow x=-\frac 14

Direttrice: y=-\frac {1-\Delta}{4a} \rightarrow y=1

Intersezioni con gli assi (ottenute sostituendo 0 alle incognite):

A(0;-1)

B(-1;0)

C(\frac 12;0)

2) Avendo l’asse di simmetria parallelo all’asse y avrà equazione:

x=ay^2+by+c

Verifichiamo le condizioni di passaggio per i 3 puni:

A(1,4) \rightarrow 1=16a+4b+c

B(-2,-5) \rightarrow -2=25a-5b+c

C(0,3) \rightarrow 0=9a+3b+c

Mettiamo tutto a sistema e otteniamo:

    \[\begin{cases} 16a+4b+c=1 \\ 25a-5b+c=-2 \\ 9a+3b+c=0 \end{cases}\]

Eseguendo la sottrazione tra la prima e la seconda e la prima e la terza otteniamo:

    \[\begin{cases} -9a+9b=3 \\ 7a+b=1 \\ 9a+3b+c=0\end{cases}\]

    \[\begin{cases} -3a+3b=1 \\ b=1-7a \\ c=-9a-3b \end{cases}\]

    \[\begin{cases} -3a+3(1-7a)=1 \\ b=1-7a \\ c=-9a-3b \end{cases}\]

    \[\begin{cases} -3a+3-21a=1 \\ b=1-7a \\c=-9a-3b \end{cases}\]

    \[\begin{cases} 24a=2 \\ b=1-7a \\ c=-9a-3b \end{cases}\]

    \[\begin{cases} a=\frac {1}{12} \\ b=1-7 \frac {1}{12} \\ c=-9a-3b \end{cases}\]

    \[\begin{cases} a=\frac {1}{12} \\ b= \frac {5}{12} \\ c=-\frac {9}{12}-\frac {15}{12} \end{cases}\]

    \[\begin{cases} a=\frac {1}{12} \\ b= \frac {5}{12} \\ c=-2 \end{cases}\]

L’equazione sarà quindi:

x=\frac {1}{12}y^2+\frac {5}{12}y-2

3)Per trovare la retta x+y=k tangente alla parabola y=1-x^2 bisognerà metterle a sistema e imporre che il \Delta sia uguale a 0.

Avremo quindi:

    \[\begin{cases} x+y=k \\ y=1-x^2\end{cases}\]

    \[\begin{cases} y=k-x \\ x^2-x+k-1=0\end{cases}\]

\Delta=1-4(k-1)=1-4k+4=5-4k

Affinchè quindi la retta sia tangente deve verificarsi che k=\frac 54, e la retta tangente sarà:

    \[x+y=\frac 54.\]

 

4) y=(k+1)x^2-3kx-4

 

  • Affinchè passi per 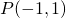P(-1,1) basterà sostituire le coordinate del punto nell’equazione così da ottenere:

1=k+1+3k-4

4k=4

k=1

  • Affinchè abbia il fuoco nel punto di ascissa 3, deve verificarsi che: 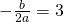-\frac {b}{2a}=3, da cui:

-\frac {-3k}{2(k+1)}=3

3k=6k+6

3k=-6

k=-2

 

 

(Questa pagina è stata visualizzata da 85 persone)

Lascia un commento