Esercizio 1 Matematica Generale

Pubblicato il da Edo1 commento
0

Dato il sistema lineare:

    \[\begin{cases} \lambda x +y+ \lambda z = 1 \\ x + \lambda y - z = \lambda \\ \lambda x + \lambda y - z = \lambda \end{cases}\]

dire se esistono valori di \lambda \in \mathbb{R} tali che:

  • non esistano soluzioni
  • esistono infinite soluzioni
  • calcolare le eventuali soluzioni per \lambda=0

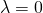
Risposta dello staff

 

 

    \[\begin{bmatrix} 1 & 1 & \lambda \\ 1 & \lambda & -1 \\ \lambda & \lambda & -1\end{bmatrix}\]

Calcoliamo il determinante della matrice, e triangolarizziamo la matrice sottraendo alla seconda riga la prima e alla terza la prima moltiplicata per \lambda.

Così otteniamo:

    \[\begin{bmatrix} 1 & 1 & \lambda \\ 0 & \lambda-1 & -1-\lambda \\ 0 & 0 &-1-\lambda^2 \end{bmatrix}\]

Il determinante sarà:

\Delta=(1-\lambda)(\lambda^2+1)

Quindi, per \lambda \neq 1, il sistema ammetterà un’unica soluzione.

Sostituiamo questo valore nel sistema e otteniamo:

    \[\begin{cases} x +y+ z = 1 \\ x + y - z = 1 \\ x + y - z =1 \end{cases}\]

Le due matrici, completa e incompleta avranno rango 2, quindi questo sistema ammetterà sempre soluzioni.

Se \lambda \neq 1 ne ammetterà solo 1.

Se \lambda = 1 ne ammetterà infinite.

    \[\begin{bmatrix} 1 & 1 & 1 \\ 1 & 1 & -1 \\ 1 & 1 & -1\end{bmatrix}.\]

Proviamo a trovare le soluzioni con \lambda=0. Il sistema diventerebbe:

    \[\begin{cases} y = 1 \\ x - z =0 \\ z = 0 \end{cases}\]

da cui:

    \[\begin{cases} y = 1 \\ x =0 \\ z = 0 \end{cases}\]

 

(Questa pagina è stata visualizzata da 81 persone)

Un pensiero riguardo “Esercizio 1 Matematica Generale”

  1. Pingback: Luca scrive: Esercizi Matematica generale | Matebook

Lascia un commento