Fabio scrive:Geometria analitica

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: Geometria analitica

Corpo del messaggio:
Dato il triangolo di vertici A(-4;3) B(-6;-3) e C(0;-5)?
Determina : a )equazione circonferenza circoscritta
b)Le equazioni delle tangenti alla circonferenza perpendicolari alla retta di equazione x-2y-9=0
c)l’area del parallelogramma individuato dalle tangenti precedenti e dalle rette di equazioni y=3 e y=-7

[soluzioni: a)x^2+y^2+4x+2y-15=0; b) 2x+y+15=0 e 2x+y-5=0; c) 100]

Risposta dello staff

a) Per calcolare l’equazione della circonferenza circoscritta risolviamo il sistema imponendo che la circonferenza (di equazione x^2+y^2+ax+by+c=0) passerà per i tre vertici:

\begin{cases} 16+9-4a+3b+c=0 \\ 36+9-6a-3b+c=0 \\ 25-5b+c=0\end{cases}

\begin{cases} 25-4a+3b+5b-25=0 \\ 45-6a-3b+5b-25=0 \\ c=5b-25\end{cases}

\begin{cases} -4a+8b=0 \\ -6a+2b+20=0 \\ c=5b-25\end{cases}

\begin{cases} a=2b \\ -12b+2b+20=0 \\ c=5b-25\end{cases}

\begin{cases} a=4 \\ b=2 \\ c=-15\end{cases}

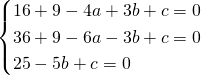
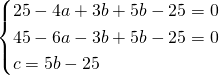
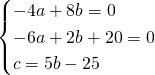
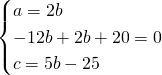
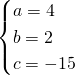
L’equazione sarà quindi:

x^2+y^2+4x+2y-15=0

b) Le rette perpendicolari alla retta data saranno del tipo:

2x+y+c=0

Per calcolare i valori di c, cerchiamo le intersezioni della retta con la circonferenza, e di seguito, poniamo il \Delta=0:

\begin{cases} x^2+y^2+4x+2y-15=0 \\ 2x+y+c=0 \end{cases}

\begin{cases} x^2+(-2x-c)^2+4x+2(-2x-c)-15=0 \\ y=-2x-c \end{cases}

\begin{cases} x^2+4x^2+4cx+c^2+4x-4x-2c-15=0 \\ y=-2x-c \end{cases}

\begin{cases} 5x^2+4cx+c^2-2c-15=0 \\ y=-2x-c \end{cases}

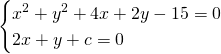
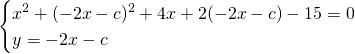
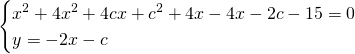
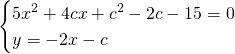
Calcoliamo il \Delta e imponiamo l’uguaglianza a 0:

\Delta=16c^2-20(c^2-2c-15)=0

16c^2-20c^2+40c+300=0

-4c^2+40c+300=0

c^2-10c-75=0

(c-15)(c+5)=0

Quindi le due rette saranno:

2x+y+15=0

2x+y-5=0

3) Calcoliamo i vertici del parallelogrammo:

A(-9;3)

B(-4;-7)

C(6;-7)

D(1;3)

Per calcolare l’area basterà notare che possiamo considerare la distanza tra A e B come base e la distanza tra B e C come altezza.

Facendo così calcoliamo semplicemente l’area con il loro prodotto:

A=\left|3-(-7)\right| \cdot \left|-4-6\right|=10\cdot 10=100

 

(Questa pagina è stata visualizzata da 58 persone)

Lascia un commento