Leandro scrive: Esercizi sulla circonferenza

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: Esercizi sulla circonferenza

Corpo del messaggio:

img068

 

Risposta dello staff

 

1) I centri sono:

C_1\left(3;0\right)

C_2\left(-1;0\right)

Sapendo che ambedue passano per l’origine (punto di contatto e quindi di conseguenza ammette immediatamente x=0 come tangente comune), avremo che i raggi sono 3 e 1.

Avremo quindi per la prima retta:

3=\frac {\left| -3m-q \right|}{\sqrt{1+m^2}}

9+9m^2=9m^2+6mq+q^2

q^2+6mq-9=0

m=\frac {9-q^2}{6q}

e sostituendo nella seconda:

1=\frac {\left| m-q \left|}{\sqrt{1+m^2}}

1+m^2=m^2-2mq+q^2

q^2-2mq-1=0

q^2-2q\frac {9-q^2}{6q}-1=0

3q^2-(9-q^2)-3=0

4q^2-12=0

q= \pm \sqrt 3

da cui:

q= \sqrt 3 \rightarrow m=\frac {9-3}{6\sqrt 3}=\frac {\sqrt 3}{3}

q= -\sqrt 3 \rightarrow m=\frac {9-3}{-6\sqrt 3}=-\frac {\sqrt 3}{3}

Le due rette saranno quindi:

y=\frac {\sqrt 3}{3}x+\sqrt 3 \quad \wedge \quad y=-\frac {\sqrt 3}{3}x-\sqrt 3

 

2) Sapendo che l’equazione di una circonferenza è:

x^2+y^2+ax+by+c=0

Risolviamo il sistema imponendo il passaggio per i 3 punti:

\begin{cases} 1+4-a+2b+c=0 \\ 9+4+3a+2b+c=0 \\ 25+16+5a+4b+c=0 \end{cases}

\begin{cases} -a+2b+c=-5 \\ 3a+2b+c=-13 \\ 5a+4b+c=-41 \end{cases}

\begin{cases} 4a=-8 \\ 3a+2b+c=-13 \\ 5a+4b+c=-41 \end{cases}

\begin{cases} a=-2 \\ -6+2b+c=-13 \\ -10+4b+c=-41 \end{cases}

\begin{cases} a=-2 \\ +2b+c=-7 \\ 4b+c=-31 \end{cases}

\begin{cases} a=-2 \\ +2b+c=-7 \\ 2b=-24 \end{cases}

\begin{cases} a=-2 \\ +2b+c=-7 \\ b=-12 \end{cases}

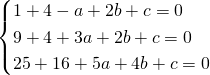
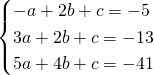
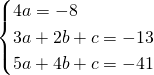
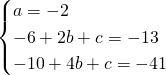
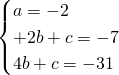
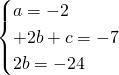
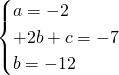
Per la richiesta non è importante trovare c in quanto le coordinate del centro saranno:

C \left( -\frac a2 ; - \frac b2\right)

Di conseguenza l’ordinata del centro sarà:

y_C=-\frac b2=6

 

 

(Questa pagina è stata visualizzata da 124 persone)

Lascia un commento