Oggetto: aiuto problema

Corpo del messaggio:
l’ipotenusa di un triangolo rettangolo misura 50a e la somma dei cateti e dell’altezza relativa all’ipotenusa misura 94a Determina i cateti ( 30a e 40 a)

 

Risposta dello staff

Sappiamo che, chiamando x e y i due cateti e h l’altezza:

Sappiamo anche che:

Di conseguenza ricaviamo l’altezza in funzione dei cateti:

Quindi avremo un sistema:

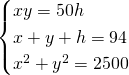
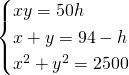
Elevando al quadrato la seconda otteniamo:

E sostituiamo ciò che abbiamo nelle altre due equazioni così da ottenere:

Svolgendo i calcoli otteniamo:

da cui l’unica soluzione accettabile è

.

Di conseguenza avremo che:

con

Sostituendo otteniamo:

Le soluzioni sono ambedue accettabili perchè è indifferente quale cateto venga scelto.

Quindi avremo:

o viceversa.

(Questa pagina è stata visualizzata da 79 persone)