Leandro scrive: Esercizio sulla retta

Pubblicato il 2 Maggio 2014 da Lo StaffLascia un commento

Oggetto: Esercizi sulla retta

Corpo del messaggio:

Risposta dello staff

1)

$2x-3y-k(x-4y+5)=0$

$x(2-k)-y(3-4k)-5k=0$

Poniamo il coefficiente angolare uguale a 3:

$\frac {2-k}{3-4k}=3$

$\frac {2-k}{3-4k}-3=0$

$\frac {2-k-9+12k}{3-4k}=0$

$11k=7$

$k=\frac {7}{11}$

Sostituendo nell’equazione otteniamo:

$x(2-\frac{7}{11})-y(3-4\frac{7}{11})-5\frac{7}{11}=0$

$\frac{15}{11}x-\frac{5}{11}y-\frac{35}{11}=0$

$3x-y-7=0$

2)

Prendiamo la generica retta:

$3x-2y+6-k(x-5y+2)=0$

$x(3-k)-y(2-5k)+6-2k=0$

Sapendo la distanza retta punto usiamo la formula e otteniamo:

$\frac {\left| 2 (3-k)+3(2-5k)+6-2k \right|}{\sqrt{(3-k)^2+(2-5k)^2}}=5$

$\frac {\left| 6-2k+6-15k+6-2k\right|}{\sqrt{(3-k)^2+(2-5k)^2}}=5$

Elevando tutto al quadrato otteniamo:

$(19k-18)^2=25(9-6k+k^2+4-20k+25k^2)$

$361k^2-684k+324=650k^2-650k+325$

$289k^2+34k+1=0$

$(17k+1)^2=0$

$k=-\frac {1}{17}$

Sostituendo nell’equazione otteniamo:

$x(3+\frac {1}{17})-y(2+5\frac {1}{17})+6+2\frac {1}{17}=0$

$\frac {52}{17}x-\frac {39}{17}y+\frac {104}{17}=0$

$4x-3y+8=0$

3)

Ricaviamo il punto di intersezione nelle prime due rette:

$\begin{cases} 3x-2y-3=0 \\ y-4x-1=0 \end{cases}$

$\begin{cases} 3x-2(4x+1)-3=0 \\ y=4x+1 \end{cases}$

$\begin{cases} 3x-8x-2-3=0 \\ y=4x+1 \end{cases}$

$\begin{cases} -5x-5=0 \\ y=4x+1 \end{cases}$

$\begin{cases} x=-1 \\ y=-3 \end{cases}$

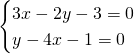
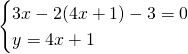
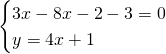
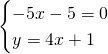
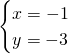
Sostituendo nella terza otteniamo:

$-1-3+k=0$

$k=4$

(Questa pagina è stata visualizzata da 108 persone)

Lascia un commento Annulla risposta

Devi essere connesso per inviare un commento.