Valentina scrive: problema di geometria ad una incognita

Pubblicato il da Lo Staff5 commenti
-1

Oggetto: problema di geometria ad una incognita.

Corpo del messaggio:
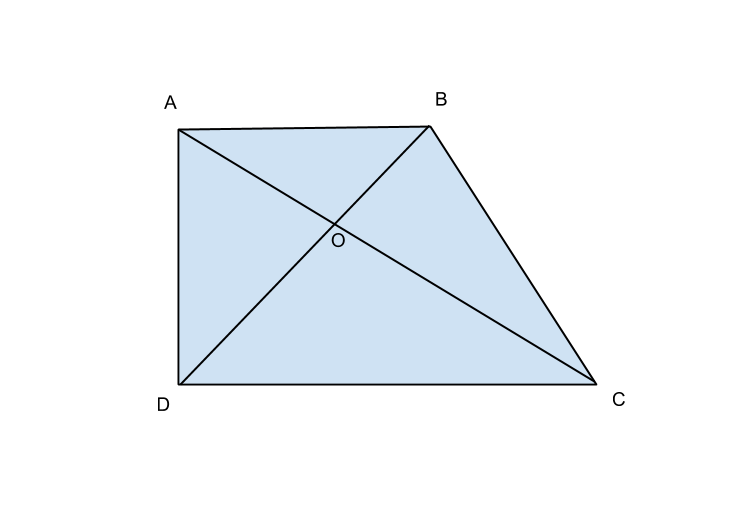
le diagonali di un trapezio rettangolo sono perpendicolari. sapendo che l’altezza è 6rad3 cm e la base maggiore è 12rad3 cm, determina la lunghezza delle diagonali.

 

Risposta dello staff

trapezio rettangolo (1)

Dai dati abbiamo che:

AD= 6\sqrt 3 \mbox{ cm}

DC=12\sqrt 3 \mbox{ cm}

La diagonale AC la ricaviamo subito con il teorema di Pitagora:

AC=\sqrt{AD^2+DC^2}=\sqrt{108+432} \mbox{ cm}=6\sqrt{15}\mbox{ cm}

Possiamo ricavare AO con il teorema di Euclide, sapendo che ADC è retto e le due diagonali perpendicolari:

AO=\frac{AD^2}{AC}=\frac {108}{6\sqrt {15}} \mbox{ cm}=\frac 65\sqrt{15} \mbox{ cm}

Ricaviamo DO con Pitagora:

DO=\sqrt{AD^2-AO^2}=\sqrt{108-\frac{540}{25}} \mbox{ cm}=\sqrt{\frac{2160}{25}} \mbox{ cm}=\frac {12}{5} \sqrt{15}\mbox{ cm}

Ricaviamo DB per Euclide:

DB=\frac{AD^2}{DO}=\frac {108}{\frac {12}{5}\sqrt {15}} \mbox{ cm}=3\sqrt{15} \mbox{ cm}

 

N.B. Si può risolvere anche con i triangoli simili, visto che per costruzione, tutti i triangoli rettangoli che si vengono a creare sono simili tra di loro.

 

(Questa pagina è stata visualizzata da 615 persone)

5 pensieri riguardo “Valentina scrive: problema di geometria ad una incognita”

  1. Grazie per la spiegazione, ma non ho ben capito come porre le lettere sul disegno che devo rappresentare.

    Rispondi

    1. Scusatemi ancora se vi disturbo, ma 12rad3 è la base maggiore quindi nel disegno dvrebbe corrispondere ad AB. Per quale motivo corrisponde a DC, ovvero la base minore? Scusatemi ma mi sto preparando per un imminente compito in classe. Sareste così gentili da togliermi questo dubbio? Grazie.

      Rispondi

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *