Valentina scrive: Problema con incognita

Pubblicato il 10 Maggio 2014 da Lo StaffLascia un commento

Oggetto: Problema con incognita.

Corpo del messaggio:
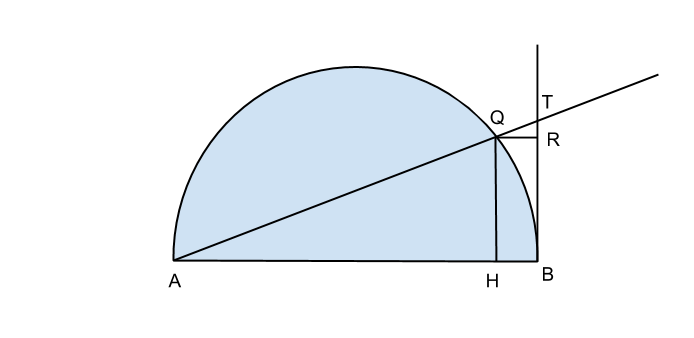
E’ data la semicirconferenza di diametro AB lungo 20 cm. Preso sulla semicirconferenza un punto Q, prolunga AQ in modo che incontri la tangente alla semicirconferenza passante per B nel punto T. Siano R e H rispettivamente le proiezioni di Q su TB e su AB.
a) Determina AQ sapendo che:
10 QR + 3 AQ = 120.
b) Trova il rapporto di similitudine tra i triangoli QTR e QBR.

Grazie.

Risposta dello staff

Dalla costruzione sapiamo che $QR=HB$ .

Sappiamo anche che, per costruzione, AQB è rettangolo perchè è inscritto in una semicirconferenza.

Quindi, sia:

$AQ=x$

AQB e AQH sono simili, e quindi avremo che:

$AH:AQ=AQ:20$

$AH=\frac {x^2}{20}$

$HB=QR=AB-AH=20-\frac {x^2}{20}$

sostituendo il tutto nell’equazione data otteniamo:

$10(20-\frac {x^2}{20})+3x=120$

$200-\frac {x^2}{2}+3x=120$

$x^2-6x-160=0$

$(x-16)(x+10)=0$

Da cui le due soluzioni:

$x=16$

o

$x=-10$

cn quest’ultima non accettabile.

2) Per ricavare il rapporto tra i due triangoli notiamo che nel rapporto delle due aree:

$r= \frac {A_{QRT}}{A_{QBR}}=\frac {\frac {QR \cdot RT}{2}}{\frac {QR \cdot RB}{2}}=\frac {RT}{RB}$

Ma notiamo che $QH=RB$ e quindi, notando che AQH e QRT sono simili avremo che:

$\frac {RT}{QH}=\frac {RQ}{AH}=\frac {HB}{AH}=0,5625$

dato che $AH=12,8 \mbox{ dm}$

(Questa pagina è stata visualizzata da 170 persone)

Lascia un commento Annulla risposta