Oggetto:
Corpo del messaggio:
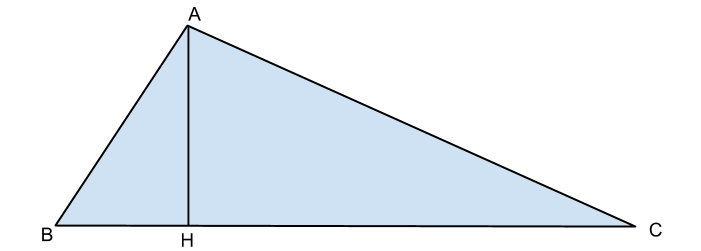
Un triangolo rettangolo in A ha il perimetro di 120 cm e il cateto AB uguale ai 5/3 della proiezione BH sull ipotenusa.
Calcola l’area del triangolo
Risposta dello staff
Dai dati avremo che:
![]()
![]()
Ponendo ![]() , otteniamo:
, otteniamo:
![]()
Per Euclide ricaviamo l’ipotenusa:
![]()
e quindi:
![]()
Ricaviamo anche il lato AC con Pitagora:
![]()
Ricaviamo quindi l’incognita:
![]()
![]()
![]()
![]()
da cui:
![]()
![]()
![]()
Calcoliamo l’area:
![]()
![]()
(Questa pagina è stata visualizzata da 85 persone)