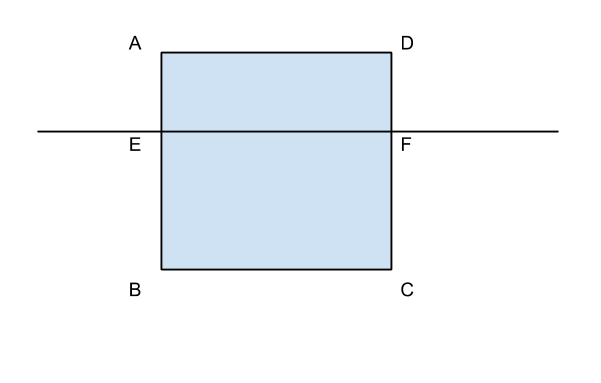
Oggetto: quadrato con lato = 5a

Corpo del messaggio:
un quadrato ha lato = 5a, una retta lo divide in due rettangoli di dimensioni diverse; il perimetro di uno è i 3/2 del perimetro dell’altro. Calcolare le due aree.

Risposta dello staff

Dalla divisione della retta, ponendo , avremo che:

Sapendo le proporzioni tra i perimetri otteniamo:

Ovviamente si poteva optare di scegliere come incognita l’altro lato, avendo come risultato .

 

(Questa pagina è stata visualizzata da 94 persone)