Lory scrive: soluzione problema geometria rapporti trapezio isoscele

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: soluzione problema geometria rapporti trapezio isoscele

Corpo del messaggio:
Aumentando di 7 cm la lunghezza dell’altezza di un trapezio, l’area aumenta di 280 cm quadrati, diminuendo di 4 cm la lunghezza di ciascuna base, l’area diminuisce di 92 cm quadrati. Calcola la lunghezza delle basi e l’area del trapezio sapendo che il rapporto tra le basi è di 7 a 13.


I risultati devono venire: 28 cm; 52 cm e 920 cm quadrati.

Risposta dello staff

Abbiamo tre incognite, e sappiamo dai dati che:

\frac {(B+b) \cdot (h+7)}{2}=\frac {(B+b) \cdot h}{2}+280

\frac {(B-4+b-4) \cdot h}{2}=\frac {(B+b) \cdot h}{2}-92

\frac bB=\frac {7}{13}

Risolviamo il sistema:

\begin{cases} \frac {(B+b) \cdot (h+7)}{2}=\frac {(B+b) \cdot h}{2}+280 \\ \frac {(B-4+b-4) \cdot h}{2}=\frac {(B+b) \cdot h}{2}-92 \\ \frac bB=\frac {7}{13} \end{cases}

\begin{cases} (B+b) \cdot (h+7)=(B+b) \cdot h+560 \\ (B+b-8) \cdot h=(B+b) \cdot h-184 \\ b=\frac {7}{13} B\end{cases}

\begin{cases} \frac {20}{13} B \cdot (h+7)=\frac {20}{13} B \cdot h+560 \\ (\frac {20}{13} B-8) \cdot h=\frac {20}{13} B \cdot h-184 \\ b=\frac {7}{13} B\end{cases}

\begin{cases} \frac {20}{13} Bh + \frac {140}{13} B=\frac {20}{13} Bh+560 \\ \frac {20}{13} Bh-8 h=\frac {20}{13} B \cdot h-184 \\ b=\frac {7}{13} B\end{cases}

\begin{cases} \frac {140}{13} B=560 \\ -8 h=-184 \\ b=\frac {7}{13} B\end{cases}

\begin{cases} B=52 \mbox{ cm} \\ h=23 \mbox{ cm} \\ b= 28 \mbox{ cm}\end{cases}

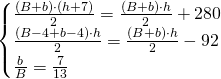
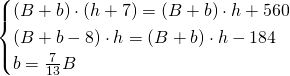
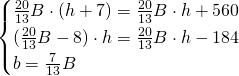
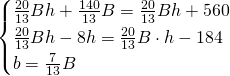
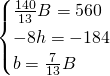
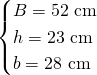
Calcoliamo l’area del trapezio iniziale:

A= \frac {(52+28) \cdot 23}{2} \mbox{ cm}^2=920 \mbox{ cm}^2

(Questa pagina è stata visualizzata da 84 persone)

Lascia un commento