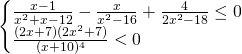
Risposta dello staff
analizziamo singolarmente i due pezzi:
![]()
![]()
![]()
![]()
![]()
![]()
La soluzione della prima disequazione è quindi:
![]() .
.
Nella seconda disequazione:
![]()
il denominatore è sempre positivo a meno di ![]() che lo annullerebbe.
che lo annullerebbe.
Uno dei due fattori del numeratore è sempre positivo, e quindi rimane solo da studiare:
![]()
La seconda disequazione è verificata quindi per
![]()
Da qui, intersecando le due soluzioni, avremo che la soluzione del sistema è:
![]()
(Questa pagina è stata visualizzata da 79 persone)
Un pensiero riguardo “Esercizio 2 Martina”