Patrizia scrive: Problema sulla circonferenza 61

Scrivi l’equazione della circonferenza che passa per i punti (4;0) e (-2;2), e che ha il centro sulla retta di equazione $3x-2y-1=0$ .

Risposta dello staff

La generica equazione di una circonferenza ha equazione:

$x^2+y^2+ax+by+c=0$

Risolviamo quindi il sistema sfruttando il passaggio per i punti, e sapendo che le coordinate del centro sono $C(-\frac a2; -\frac b2)$ , avremo, sfruttand l’equazione della retta su cui giace il centro:

$-\frac 32 a +b-1=0$ .

Risolviamo il sistema:

$\begin{cases} 16+4a+c=0 \\ 4+4-2a+2b+c=0 \\-3a+2b-2=0 \end{cases}$

$\begin{cases} c=-16-4a \\ 8-2a+2b-16-4a=0 \\-3a+2b-2=0 \end{cases}$

$\begin{cases} c=-16-4a \\ -6a+2b-8=0 \\-3a+2b-2=0 \end{cases}$

$\begin{cases} c=-16-4a \\ 3a-b+4=0 \\-3a+2b-2=0 \end{cases}$

$\begin{cases} c=-16-4a \\ b=3a+4 \\-3a+6a+8-2=0 \end{cases}$

$\begin{cases} c=-16-4a \\ b=3a+4 \\3a=-6 \end{cases}$

$\begin{cases} c=-8 \\ b=-2 \\ a=-2 \end{cases}$

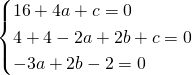
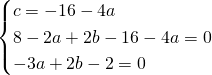
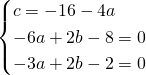
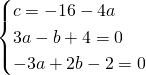
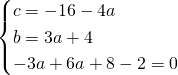
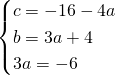
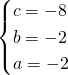
L’equazione sarà quindi:

$x^2+y^2-2x-2y-8=0$

(Questa pagina è stata visualizzata da 78 persone)

Matebook

La matematica spiegata passo passo

Patrizia scrive: Problema sulla circonferenza 61

Risposta dello staff

Un pensiero riguardo “Patrizia scrive: Problema sulla circonferenza 61”

Lascia un commento Annulla risposta