Piero scrive: problema semicirconferenza

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: problema geometrico grafico

Corpo del messaggio:
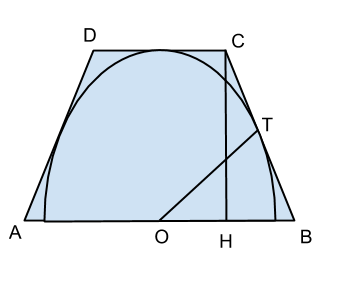
circoscrivere ad una semicirconferenza di raggio r, un trapezio isoscele con perimetro 2kr.

trapezio e semicirconferenza

 

 Risposta dello staff

Sappiamo che in un trapezio isoscele circoscritto ad una semicirconferenza, il lato obliquo è uguale alla metà della base maggiore.

Quindi avremo che:

AO=OB=AD=CB=x

Ricaviamo HB con Pitagora per calcolare la base minore:

HB=\sqrt{x^2-r^2}

Quindi avremo che:

DC=2x-2\sqrt{x^2-r^2}

Avremo quindi il perimetro:

2p=2x+x+x+2x-2\sqrt{x^2-r^2}

da cui:

6x-2\sqrt{x^2-r^2}=2kr

3x-kr=\sqrt{x^2-r^2}

9x^2-6krx+k^2r^2=x^2-r^2

8x^2-6krx+k^2r^2+r^2=0

8x^2-6krx+r^2(k^2+1)=0

x_{\frac 12}=\frac{6kr \pm \sqrt {36k^2r^2-32r^2(k^2+1)}}{16}=\frac{6kr \pm \sqrt {4k^2r^2-32r^2}}{16}

x_{\frac 12}=\frac{6kr \pm 2r\sqrt {k^2-8}}{16}=\frac{3kr \pm r\sqrt {k^2-8}}{8}

Studiamo ora, considerando che x \geq r, quali sono i valori di k accettabili:

\frac{3kr \pm r\sqrt {k^2-8}}{8}\geq r

3k \pm \sqrt {k^2-8}\geq 8

\pm \sqrt {k^2-8}\geq 8-3k

\sqrt {k^2-8}\geq 8-3k \quad \lor \quad \sqrt {k^2-8}\leq 3k-8

Studiamo i due casi:

\begin{cases} 8-3k \geq 0 \\ k^2- 8 \geq 9k^2-48k+64 \end{cases} \qquad \qquad \begin{cases} 8-3k < 0 \\ k^2-8 \geq 0 \end{cases}

\begin{cases} k \leq \frac 83 \\ 8k^2-48k+72 \leq 0 \end{cases} \qquad \qquad \begin{cases} k > \frac 83 \\ k \leq -2\sqrt2 \quad \lor \quad k \geq 2\sqrt2 \end{cases}

\begin{cases} k \leq \frac 83 \\ k^2-6k+9 \leq 0 \end{cases} \qquad \qquad \begin{cases} k > \frac 83 \\ k \leq -2\sqrt2 \quad \lor \quad k \geq 2\sqrt2 \end{cases}

\begin{cases} k \leq \frac 83 \\ (k-3)^2 \leq 0 \end{cases} \qquad \qquad \begin{cases} k > \frac 83 \\ k \leq -2\sqrt2 \quad \lor \quad k \geq 2\sqrt2 \end{cases}

Il primo sistema non ammetterà soluzione, il secondo ammetterà k \geq 2\sqrt 2

 

Studiamo la seconda disequazione:

\begin{cases} k^2-8 \geq 0 \\ 3k-8 \geq 0 \\ k^2-8 \leq 9k^2-49k+64 \end{cases}

\begin{cases} k \leq -2\sqrt2 \quad \lor \quad k \geq 2\sqrt2 \\ k \geq \frac 83 \\ (k-3)^2 \geq 0 \end{cases}

Anche questa ammetterà come soluzion:

k\geq 2\sqrt 2

Unendo le due soluzioni otteniamo che la soluzione sarà:

k \leq \frac 52.

Notiamo però che, essendo il perimetro uguale a 2kr ed il diametro, ovvero la base maggiore, uguale ad r, allora k deve essere necessariamente maggiore di 1 e quindi:

1 <k \leq \frac 52

 

(Questa pagina è stata visualizzata da 104 persone)

Lascia un commento