Maria chiara scrive: numeri

Pubblicato il da Lo StaffLascia un commento
0

Corpo del messaggio:
Trova due numeri sapendo che la metà del primo supera di 32 il quintuplo del secondo mentre la metà del triplo del primo supera di 45 il secondo moltiplicato per 7.

Risposta dello staff

Chiamiamo x e y i due numeri ed avremo:

\begin{cases} \frac 12x = 32 +5y \\ \frac 32 x=45+ 7y \end{cases}

\begin{cases} x = 64 +10y \\ 3 x=90+ 14y \end{cases}

\begin{cases} x = 64 +10y \\ 3 (64+10y)=90+ 14y \end{cases}

\begin{cases} x = 64 +10y \\ 192+30y=90+ 14y \end{cases}

\begin{cases} x = 64 +10y \\ 16y=-102 \end{cases}

\begin{cases} x = 64 +10y \\ y=-\frac{51}{8} \end{cases}

\begin{cases} x = 64 -\frac{255}{4} \\ y=-\frac{51}{8} \end{cases}

\begin{cases} x = \frac{1}{4} \\ y=-\frac{51}{8} \end{cases}

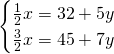
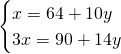
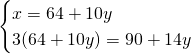
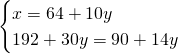
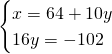
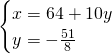
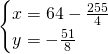
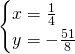
(Questa pagina è stata visualizzata da 73 persone)

Lascia un commento