Oggetto: sistemi di 2 equazioni di 1^ grado in 2 incognite
Corpo del messaggio:
risolvere la seguente equazione con i 4 metodi algebrici + quello grafico :
{x+y=3
{5x – 4y = 3
Risposta dello staff
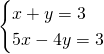
- Metodo di sostituzione
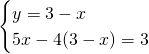
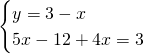
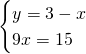
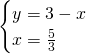
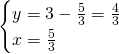
- Metodo di confronto:
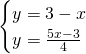
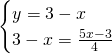
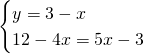
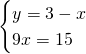
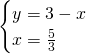
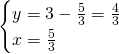
- Metodo di riduzione:
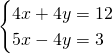
Sommiamo la seconda riga alla prima e otteniamo:
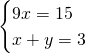
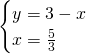
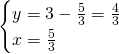
- Metodo di Cramer:
![]()
![]()
![]()
![]()
![]()
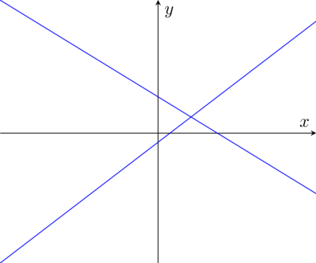
- Metodo Grafico
(Questa pagina è stata visualizzata da 58 persone)