Matteo scrive: Problema sul trapezio

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: Ho bisogno di aiuto su questo problema 🙂 grazie

Corpo del messaggio:
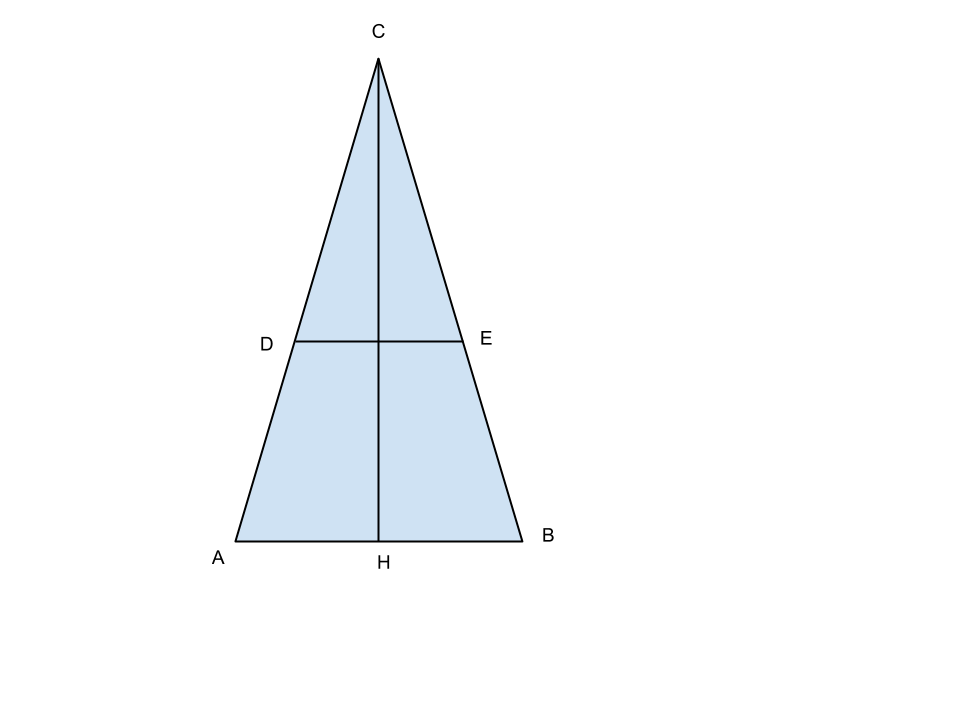
Prolungando i lati non paralleli del trapezio ABED fino fino ad incontrarsi nel punto C si è ottenuto il triangolo ECD. Sapendo che la base maggiore del trapezio misura 30 cm ed è i 10/7 della minore e i 5/2 dell’altezza. Calcola perimetro ed area del triangolo ECD.

 

Risposta dello staff

triangolo isoscele con corda

 

 

Dai dati ricaviamo subito la base minore e l’altezza:

b=\frac{7}{10}B=21 \mbox{ cm}

h=\frac 25 B=12 \mbox{ cm}

Ricaviamo l’altezza del triangolo ACB:

AB:DE=CH:CK

Chiamando CK=x avremo:

\frac {10}{7}=\frac{x+12}{x}

10x=7x+84

3x=84

x=28 \mbox{ cm}

Sapendo quindi l’altezza del triangolo CDE, calcoliamo l’area:

A_{CDE}=\frac {21 \cdot 28}{2}\mbox{ cm}^2=294 \mbox{ cm}^2

Ora, con le similitudini, possiamo ricavare i due lati del triangolo:

AC:CD=CH:CK

Chiamando CD=x avremo:

*** QuickLaTeX cannot compile formula:
 

*** Error message:
Error: Nothing to show, formula is empty

AC:CD=CH:CKChiamandoCK=x$ avremo:

(Questa pagina è stata visualizzata da 106 persone)

Lascia un commento