Oggetto:

Corpo del messaggio:
La diagonale BD divide il pentagono nelrettangolo ABDE e nel triangolo BCD (angolo retto in C)
la diagonale del rettangolo è lunga 24 cm.
L’area di BCDè 54cm2
La lunghezza di BC è 3\8 di quella della diagonale del rettangolo.
Calcola il perimetro del pentagono ( approssima ai mm)
Aiuto! Come faccio?

Risposta dello staff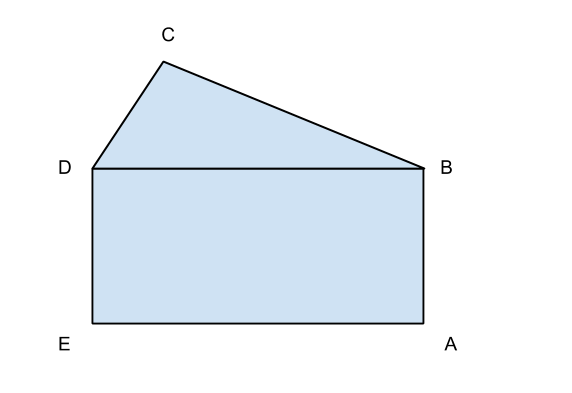

Dai dati ricaviamo subito la lunghezza di BC:

Ora, sapendo l’area del triangolo, ricaviamo anche CD:

Ricaviamo BD con il teorema di Pitagora:

Conoscendo BD e la diagonale BE, ricaviamo anche l’altro lato del rettangolo con il teorema di Pitagora:

Abbiamo tutti i dati per calcolare il perimetro:

(Questa pagina è stata visualizzata da 49 persone)