Francesco scrive: Esercizio sul trapezio

Pubblicato il 29 Gennaio 2015 da Lo StaffLascia un commento

Oggetto:

Corpo del messaggio:
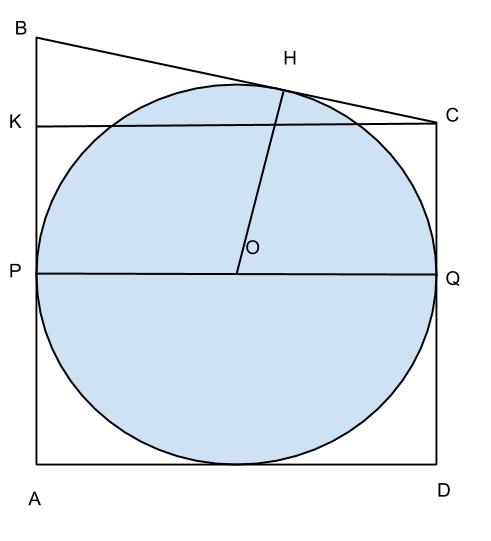
Determinare il perimetro e l’area di un trapezio rettangolo circoscritto ad una circonferenza che tocca il lato obliquo in un punto distante cm 9 e cm 16 dagli estremi di detto lato.
RISULTATI: [98;588]

Risposta dello staff

Essendo il trapezio circoscritto ad una circonferenza, sappiamo che la somma dei lati opposti è uguale ed sono anche uguali i segmenti tangenti alla circonferenza.

Quindi avremo:

$CB=25 \mbox{ cm}$

$HB=BP=16 \mbox{ cm}$

$HC=CQ=9 \mbox{ cm}$

Ricaviamo ora CK con il teorema di Pitagora, sapendo che:

$BK=(16-9)\mbox{ cm}=7\mbox{ cm}$

$CK=\sqrt{BC^2-BK^2}=\sqrt{625-49} \mbox{ cm}=\sqrt{576}\mbox{ cm}=24 \mbox{ cm}$

$CK=AD$

Quindi, chiamando $AP=DQ=12\mbox{ cm}$ .

Ora che abbiamo tutti i dati, troviamo il perimetro:

$2p=(28+25+21+24)\mbox{ cm}=98\mbox{ cm}$

L’area sarà:

$A=\frac{(28+21) \cdot 24}{2}\mbox{ cm}^2=588 \mbox{ cm}^2$

(Questa pagina è stata visualizzata da 100 persone)

Lascia un commento Annulla risposta