Claudio scrive: Problemi con la parabola 240

Pubblicato il da EdoLascia un commento
-1

Scrivi l’equazione della parabola che ha il fuoco in F\left(2;-\frac 34\right) e ha come direttrice la retta di equazione y=-\frac 54. Indica con A e B (x_A<x_B) i punti di intersezione della parabola con la retta di equazione y=2x+1. Determina l’area del trapezio AA'B'B, essendo A’ e B’ le proiezioni di A e B sull’asse x.

 

Risposta dello staff

La generica equazione della parabola è:

y=ax^2+bx+c

e, dalla traccia avremo:

\begin{cases} -\frac{b}{2a}=2 \\ \frac{1-b^2+4ac}{4a}=-\frac 34 \\ -\frac{1+b^2-4ac}{4a}=-\frac 54 \end{cases}

\begin{cases} b=-4a \\ 1-b^2+4ac=-3a \\ -1-b^2+4ac=- 5a \end{cases}

\begin{cases} b=-4a \\ 1-b^2+4ac=-3a \\ 2=2a \end{cases}

\begin{cases} b=-4 \\ 1-b^2+4c=-3 \\ a=1 \end{cases}

\begin{cases} b=-4 \\ 1-16+4c=-3 \\ a=1 \end{cases}

\begin{cases} b=-4 \\ c=3 \\ a=1 \end{cases}

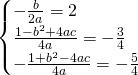
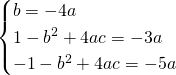
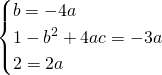
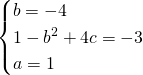
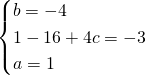
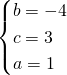
L’equazione sarà quindi:

y=x^2-4x+3

Troviamo i due punti di intersezione:

\begin{cases} y=x^2-4x+3 \\ y=2x+1 \end{cases}

\begin{cases} 2x+1=x^2-4x+3 \\ y=2x+1 \end{cases}

\begin{cases} x^2-6x+2=0 \\ y=2x+1 \end{cases}

da cui:

x_{\frac 12}=\frac{6 \pm \sqrt{36-8}}{2}=\frac{6 \pm 2\sqrt{7}}{2}=3 \pm \sqrt 7

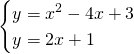
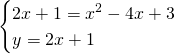
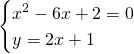
da cui i punti:

A(3-\sqrt7;7-2\sqrt 7)

B(3+\sqrt7;7+2\sqrt 7)

A'(3-\sqrt7;0)

B(3+\sqrt7;0)

Per calcolare l’area quindi avremo:

A=\frac{(AA'+BB') \cdot A'B'}{2}=\frac{(7-2\sqrt 7+7+2\sqrt 7)\cdot 2\sqrt 7}{2}=14\sqrt 7

 

Rendered by QuickLaTeX.com

(Questa pagina è stata visualizzata da 84 persone)

Lascia un commento