Claudio scrive: Problemi con la parabola 241

Pubblicato il da EdoLascia un commento
0

Scrivi l’equazione della parabola passante per A(1,0), B(4,0) e C(0,4). Tracciane il grafico e determina l’equazione della retta tangente alla parabola e parallela alla retta di equazione y=-2x

Risposta dello staff

La generica equazione è y=ax^2+bx+c, e quindi dati i punti dati della traccia avremo:

\begin{cases} a+b+c=0 \\ 16a+4b+c=0 \\ c=4\end{cases}

\begin{cases} a+b=-4 \\ 16a+4b=-4 \\ c=4\end{cases}

\begin{cases} b=-a-4 \\ 16a-4a-16=-4 \\ c=4\end{cases}

\begin{cases} b=-a-4 \\ 12a=12 \\ c=4\end{cases}

\begin{cases} b=-5 \\ a=1 \\ c=4\end{cases}

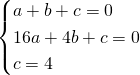
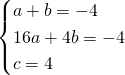
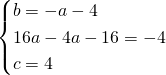
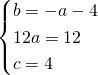
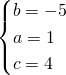
L’equazione sarà quindi:

y=x^2-5x+4

Per trovare la retta tangente parallela a quella data intersecheremo la generica retta parallela e imporremo  \Delta=0.

\begin{cases} y=x^2-5x+4 \\ y=-2x+q\end{cases}

\begin{cases} -2x+q=x^2-5x+4 \\ y=-2x+q\end{cases}

\begin{cases} x^2-3x+4-q=0 \\ y=-2x+q\end{cases}

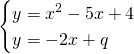
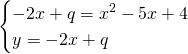
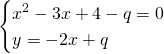
Da qui avremo:

\Delta=9-16+4q=4q-7

da cui:

4q-7=0 \iff q=\frac 74

L’equazione della retta tangente sarà quindi:

y=-2x+\frac 74

 

Rendered by QuickLaTeX.com

(Questa pagina è stata visualizzata da 92 persone)

Lascia un commento