Claudio scrive: Problemi con la parabola 242

Pubblicato il da EdoLascia un commento
0

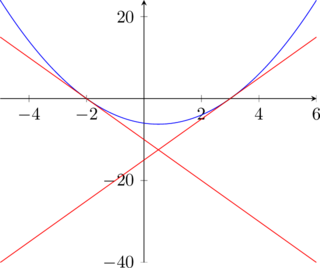
Traccia il grafico della parabola di equazione y=x^2-x-6 e determina le coordinate dei punti d’intersezione A e B con l’asse x (x_A<x_B). scrivi le equazioni delle rette tangenti alla parabola in A e B, indicando con C il loro punto di intersezione. Determina l’area del triangolo ABC.

Risposta dello staff

Troviamo subito le due intersezioni:

x^2-x-6=0

(x-3)(x+2)=0

x_A=-2

x_B=3

da cui:

A(-2;0) e B(3;0).

La generica retta passante per A è:

y=mx+2m

Imponendo le condizioni di tangenza avremo:

\begin{cases} y=x^2-x-6 \\ y=mx+2m \end{cases}

\begin{cases} mx+2m=x^2-x-6 \\ y=mx+2m \end{cases}

\begin{cases} x^2-x(m+1)-6-2m=0 \\ y=mx+2m \end{cases}

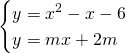
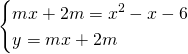
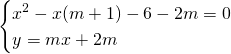
da cui:

\Delta=m^2+2m+1+24+8m=m^2+10m+25

m^2+10m+25=0 \iff m=-5

da cui:

y=-5x-10 è la retta tangente alla parabola nel punto A.

Svolgiamo nell’identico modo per il punto B

La generica retta passante per A è:

y=mx-3m

Imponendo le condizioni di tangenza avremo:

\begin{cases} y=x^2-x-6 \\ y=mx-3m \end{cases}

\begin{cases} mx-3m=x^2-x-6 \\ y=mx-3m \end{cases}

\begin{cases} x^2-x(m+1)-6+3m=0 \\ y=mx-3m\end{cases}

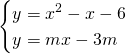
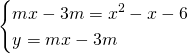
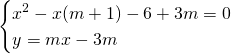
da cui:

\Delta=m^2+2m+1+24-12m=m^2-10m+25

m^2-10m+25=0 \iff m=5

da cui:

y=5x-15 è la retta tangente alla parabola nel punto B.

Troviamo le coordinate di C:

\begin{cases} y=-5x-10 \\ y=5x-15\end{cases}

\begin{cases} y=-5x-10 \\ 2y=-25\end{cases}

\begin{cases} y=-5x-10 \\ y=-\frac{25}{2}\end{cases}

\begin{cases} -5x-10=-\frac{25}{2} \\ y=-\frac{25}{2}\end{cases}

\begin{cases} 10x-20=-25 \\ y=-\frac{25}{2}\end{cases}

\begin{cases} 10x=-45 \\ y=-\frac{25}{2}\end{cases}

\begin{cases} x=-\frac 92 \\ y=-\frac{25}{2}\end{cases}

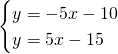
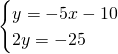
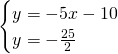
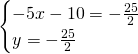
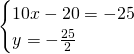
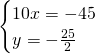
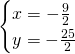
Calcoliamo l’area:

A=\frac{|x_B-x_A| \cdot |y_C|}{2}=\frac {5 \cdot\frac {25}{2} }{2}=\frac{125}{4}

 

 

 

 

 

 

 

 

Rendered by QuickLaTeX.com

(Questa pagina è stata visualizzata da 68 persone)

Lascia un commento