Scrivi l’equazione della parabola che ha vertice nel punto 
e passa per l’origine. Scrivi le equazioni delle rette tangenti alla parabola passanti per 
e indica con A e B i punti di contatto delle tangenti con la parabola. Calcola l’area del triangolo APB:
Risposta dello staff
Passando per l’origine l’equazione sarà del tipo.
da cui:
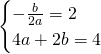
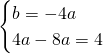
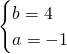
L’equazione sarà quindi:
La generica retta passante per P è :
da cui, imponendo le condizioni di tangenza avremo:
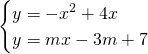
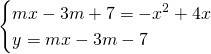
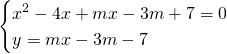
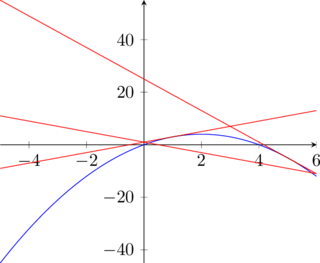
da cui le due rette sono:
e 
Ricaviamo ora i due punti di intersezione:
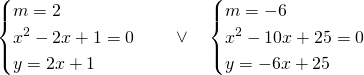
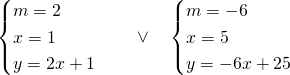
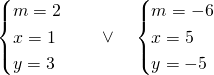
I due punti saranno quindi:
e 
Per calcolare l’area usiamo la regola di Sarrus:
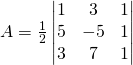
da cui:
(Questa pagina è stata visualizzata da 61 persone)