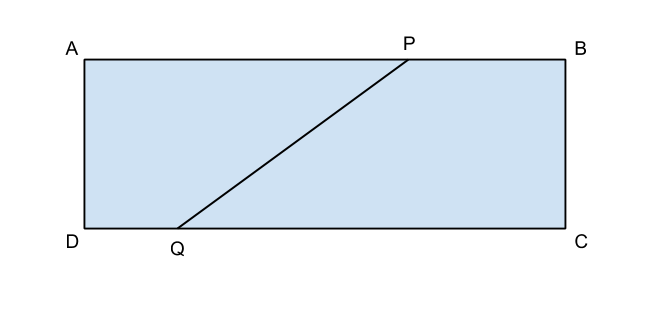
in un  rettangolo ABCD, la base AB è doppia del lato BC e il perimetro del rettangolo è 24 cm.
– determina le lunghezze di AB e di BC.
– determina un punto P su AB e un punto Q su CD tali che QC sia 2 cm in più di AP e risulti  AP+ 2/3 PB= DQ + 1/2 QC.
-determina le aree dei trapezi APQD e PBCQ

Risposta dello staff

Ricaviamo subito i lati ponendo :

da cui:

Ora, ponendo , avremo:

da cui avremo:

e quindi:

.

Ora, sapendo che l’area del rettangolo è

calcolando l’area di un trapezio ricaveremo automaticamente l’area del secondo per differenza:

e quindi:

 

(Questa pagina è stata visualizzata da 89 persone)