Oggetto: Parallelismo tra rette

Corpo del messaggio:
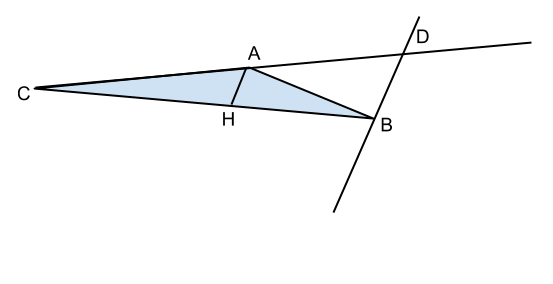
Dato il triangolo ABC, conduci dal vertice B la parallela alla bisettrice dell’angolo in A e sia D il punto in cui tale parallela interseca il prolungamento del lato AC. Dimostra che è AB=DA.

Risposta dello staff

 

Risposta dello staff

Essendo AH la bisettrice dell’angolo A avremo che:

Ora, sapendo che BD e AH sono parallele, consideriamo queste tagliate da DC, e avremo che:

perchè corrispondenti.

Ora, invece consideriamo le stesse rette parallele tagliate però da BA e avremo che:

perchè alterni interni.

Ma quindi:

o meglio:

Quindi, il triangolo ABD è isoscele e

(Questa pagina è stata visualizzata da 85 persone)