Emanuele scrive: Integrale

Oggetto: Calcolare l integrale indefinito seguente

Corpo del messaggio:
$\int \frac{3x-1}{x(x^2+3x+2)} \, \, dx$

$\int \frac{3x-1}{x(x+2)(x+1)} \, \, dx$

Riscriviamolo come:

$\frac{A}{x}+\frac{B}{x+1}+\frac{C}{x+2}=\frac{3x-1}{x(x+1)(x+2}$

$\frac{A(x^2+3x+2)+B(x^2+2x)+C(x^2+x)}{x(x+1)(x+2)}=\frac{3x-1}{x(x+1)(x+2}$

Mettendo a sistema per avere trovare i valori numerici otteniamo:

$\begin{cases} A+B+C=0 \\ 3A+2B+C=3 \\ 2A=-1 \end{cases}$

$\begin{cases} -\frac 12+B+C=0 \\ -\frac 32+2B+C=3 \\ A=-\frac 12 \end{cases}$

$\begin{cases} -\frac 12+B+C=0 \\ -1+B=3 \\ A=-\frac 12 \end{cases}$

$\begin{cases} -\frac 12+4+C=0 \\ B=4 \\ A=-\frac 12 \end{cases}$

$\begin{cases} C=-\frac 72 \\ B=4 \\ A=-\frac 12 \end{cases}$

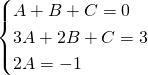
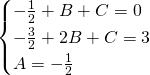
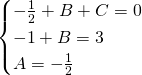
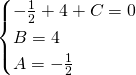
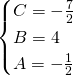
Ora quindi avremo che l’integrale diventa:

$\int \left( -\frac{1}{2x}+\frac{4}{x+1}-\frac{7}{2(x+2)} \, \, dx$

formato da solo integrali immediati la cui soluzione sarà:

$-\frac 12 log |x| + 4 log |x+1| - \frac 72 log |x+2| +C$

(Questa pagina è stata visualizzata da 62 persone)

Matebook