Leandro scrive: esercizi

Pubblicato il da Lo Staff1 commento
0

Oggetto: esercizi sul significato geometrico del coefficiente angolare di una retta

Corpo del messaggio:

img026

 

Risposta dello staff

1)

Se il coseno dell’angolo è \frac 12, ne deduciamo che l’angolo che si viene a formare è 60^\circ per cui il coefficiente angolare della retta sarà:

m=tg(60^\circ)=\sqrt 3

per cui l’equazione sarà del tipo:

y=\sqrt 3x+q

imponiamo il passaggio per P e otteniamo:

-8=3+q

q=-11

L’equazione è quindi:

y=\sqrt 3x-11

2)

y=-4x+1

Per cui avremo, chiamando con s e c le due incognite:

\begin{cases} \frac sc= -4 \\ s^2+c^2=1 \end{cases}

\begin{cases} s= -4c \\ 16c^2+c^2=1 \end{cases}

\begin{cases} s= -4c \\ 17c^2=1 \end{cases}

\begin{cases} s= -4c \\ c=\pm \frac{1}{\sqrt{17}} \end{cases}

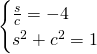
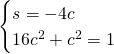
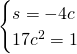
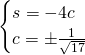
Essendo il coefficiente angolare negativo, il coseno sarà negativo e quindi

c=-\frac{1}{\sqrt{17}}

s=\frac{4}{\sqrt{17}}

3)

y=\frac 38x+\frac 78

Per cui avremo, chiamando con s e c le due incognite:

\begin{cases} \frac sc= \frac 38 \\ s^2+c^2=1 \end{cases}

\begin{cases} s= \frac 38c \\ \frac {9}{64}c^2+c^2=1 \end{cases}

\begin{cases} s= \frac 38c \\ \frac{73}{64}c^2=1 \end{cases}

\begin{cases} s= \frac 38 \\ c=\pm \frac{8}{\sqrt{73}} \end{cases}

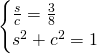
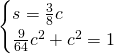
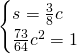
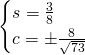
Essendo il coefficiente angolare positivo, il coseno sarà positivo e quindi

c=\frac{8}{\sqrt{73}}

s=\frac{3}{\sqrt{73}}

(Questa pagina è stata visualizzata da 70 persone)

Un pensiero riguardo “Leandro scrive: esercizi”

  1. In riferimento all’esercizio n.1 , anche il coseno di 300 gradi è 1/2 e la tangente è -radice di 3. Perché si sceglie l’angolo di 60 e non quello di 300.

    Grazie e distinti saluti

Lascia un commento