Oggetto: risolvere un problema
Corpo del messaggio:
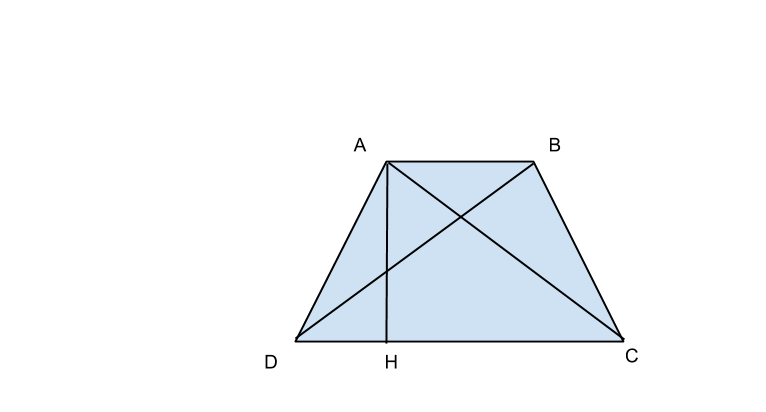
in un trapezio isoscele ABCD avente il perimetro di 62 cm e la diagonale Db è perpendicolare al lato obliquo BC. determina l area sapendo che la somma delle due basi è 32cm.
Risposta dello staff
Sapendo il perimetro e la somma delle basi, ricaviamo subito la lunghezza del lato obliquo:
![]()
Sapendo che ADC è rettangolo, utilizziamo il teorema di Euclide, ponendo ![]() ,
, ![]() per cui:
per cui:
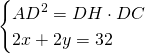
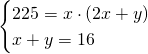
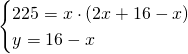
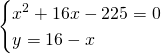
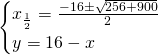
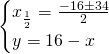
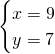
Quindi avremo che:
![]()
![]()
Ricaviamo AH con il secondo teorema di Euclide:
![]()
Calcoliamo l’area quindi:
![]()
(Questa pagina è stata visualizzata da 100 persone)