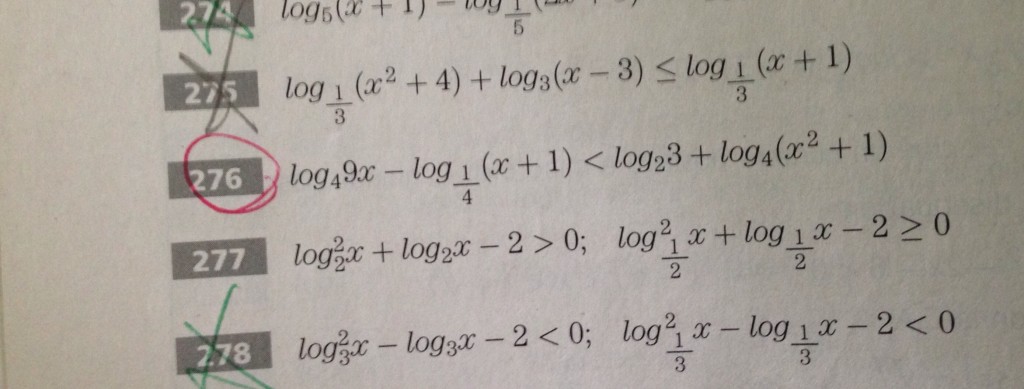Alessandro scrive: Disequazioni logaritmiche

Oggetto: Disequazioni logaritmiche

Corpo del messaggio:
Vorrei la soluzione alla numero 276 con tutti passaggi spiegati per favore ,grazie

$log_4 9x - log_{\frac 14}(x+1) < log_23+log_4(x^2+1)$

Innanzitutto vediamo il campo di esistenza, e quindi, se ammettesse soluzione, deve essere necessariamente $x>0$

Scriviamo tutto sotto la stessa base così da avere:

$log_4 9x - \frac{log_4 (x+1)}{log_{4}\frac 14} <\frac{log_4 3}{log_{4} 2}+log_4(x^2+1)$

Ora, sapendo che:

$log_{4}\frac 14=-1$

$log_{4} 2=\frac 12$

avremo:

$log_4 9x + log_4 (x+1) <2log_4 3+log_4(x^2+1)$

$log_4 (9x (x+1)) < log_4(9(x^2+1))$

per cui, dato che la base del logaritmo è maggiore di 1, avremo:

$9x(x+1)<9(x^2+1)$

$9x^2+9x<9x^2+9$

$x<1$

Per cui la soluzione finale è:

$0<x<1$

(Questa pagina è stata visualizzata da 74 persone)

Matebook