Christopher scrive: rettangolo inscritto in un triangolo

Oggetto: rettangolo inscritto in un triangolo

Corpo del messaggio:
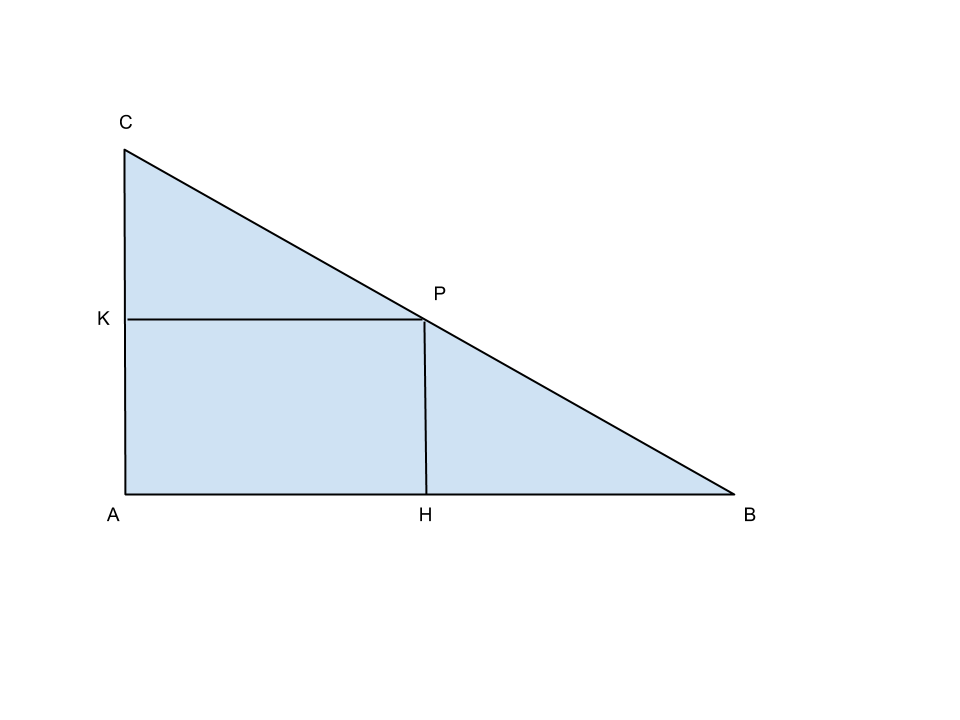
Un triangolo ABC rettangolo in A ha i cateti AB e AC rispettivamente di lunghezza 20a e 15a. Determina sull’ipotenusa un punto P in modo che, dette H e K le sue proiezioni sui cateti, il rettangolo PHAK abbia perimetro 36a.

Risposta dello staff

Dai dati abbiamo che:

$AB=20 a$

$AC=15a$

Per il teorema di Pitagora avremo che:

$BC=\sqrt{AB^2+AC^2}=\sqrt{400+225}a=25a$

Ora, chiamando BP con x, avremo:

$BP=x$

$CP=25a-x$

$BH=\frac{AB \cdot BP}{BC}=\frac{20ax}{25a}=\frac45x$

$PH=\frac{AC \cdot BP}{BC}=\frac{15ax}{25a}=\frac35x$

$PK=\frac{AB \cdot PC}{BC}=\frac{20a(25a-x)}{25a}=\frac45(25a-x)$

Da qui avremo che, considerando il semiperimetro del rettangolo:

$PH+PK=18a$

$\frac 35x + \frac 45 (25a-x)=18a$

$3x+100a-4x=90a$

$x=10a$

(Questa pagina è stata visualizzata da 65 persone)

Matebook

La matematica spiegata passo passo

Christopher scrive: rettangolo inscritto in un triangolo

Risposta dello staff

Lascia un commento Annulla risposta