Oggetto: Problema di geometria

Corpo del messaggio:
In un triangolo rettangolo  l’ipotenusa misura 30 cm e il rapporto delle proiezioni dei cattivi su di essa  è  16 / 9. Quanto misurano l’altezza relativa all’ipotenusa  e il semi perimetro del triangolo?
R.14,4cm;30 cm.

Risposta dello staff

 

 

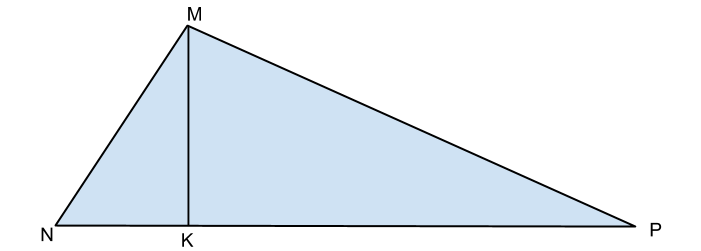
Calcoliamo subito i due segmenti in cui è diviso NP:

Conoscendo NK e KP troviamo l’altezza con il secondo teorema di Euclide:

Calcoliamo ora i due cateti con il primo teorema di Euclide:

E quindi, il semiperimetro sarà:

 

 

 

 

 

 

 

(Questa pagina è stata visualizzata da 74 persone)