Giorgio scrive: Problema da risolvere – Euclide

Pubblicato il da Lo StaffLascia un commento
-1

Oggetto: Problema da risolvere – Euclide

Corpo del messaggio:
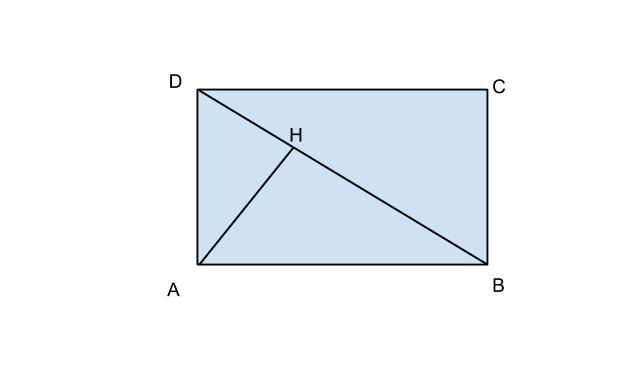
Nel rettangolo ABCD,la diagonale BD misura 95 dm ed è divisa dalla perpendicolare AH,condotta per il vertice A,in due segmenti tali che uno di essi è 9/16 dell’altro.Calcola il perimetro e l’area del rettangolo.
Grazie infinite!!!

Risposta dello staff

rettangolo con diagonale

Calcoliamo subito i due segmenti in cui è diviso BD:

BH+HD=95 \mbox{ dm}

BH+ \frac{9}{16}BH=95\mbox{ dm}

\frac{25}{16}BH=95\mbox{ dm}

BH=60,8 \mbox{ dm}

DH=34,2 \mbox{ dm}

Conoscendo BH e HD troviamo i due cateti con il primo teorema di Euclide:

AB=\sqrt{95* 60,8} \mbox{ dm}=76\mbox{ dm}

AD=\sqrt{95* 34,2} \mbox{ dm}=57\mbox{ dm}

2p=2(76+57)\mbox{ dm}=266\mbox{ dm}

A=(76 \cdot 57) \mbox{ dm}^2=4332 \mbox{ dm}^2

 

(Questa pagina è stata visualizzata da 58 persone)

Lascia un commento