Lorena scrive: Disequazione

Pubblicato il da Lo StaffLascia un commento
-2

Oggetto:

Corpo del messaggio:
1)

| x^2| - |1-x^2|>0

x^2 \geq 0 \, \, \forall x

1-x^2 \geq 0 \iff -1\leq x \leq 1

Per cui avremo:

\begin{cases} -1 \leq x \leq 1 \\ x^2-1+x^2 >0 \end{cases} \quad \quad \begin{cases} x<-1 \quad \lor \quad x> 1 \\ x^2+1-x^2 >0 \end{cases}

\begin{cases} -1 \leq x \leq 1 \\ 2x^2 >1 \end{cases} \quad \quad \begin{cases} x<-1 \quad \lor \quad x> 1 \\ 1 >0 \end{cases}

\begin{cases} -1 \leq x \leq 1 \\ x^2 >\frac 12 \end{cases} \quad \quad \begin{cases} x<-1 \quad \lor \quad x> 1 \\ 1 >0 \end{cases}

\begin{cases} -1 \leq x \leq 1 \\ x<-\frac{\sqrt 2}{2}\quad \lor \quad x>\frac{\sqrt 2}{2} \end{cases} \quad \quad \begin{cases} x<-1 \quad \lor \quad x> 1 \\ 1 >0 \end{cases}

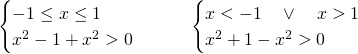
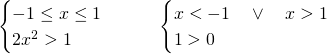
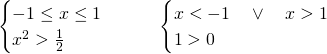
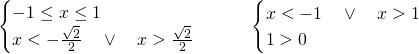
Ora, il primo sistema sarà verificato per:

-1 \leq x <-\frac{\sqrt 2}{2}\quad \lor \quad \frac{\sqrt 2}{2} <x\leq 1

Il secondo sistema sarà verificato per:

x<-1 \quad \lor \quad x>1

Per cui la soluzione della disequazione iniziale è:

x<-\frac{\sqrt 2}{2} \quad \lor \quad x>\frac{\sqrt 2}{2}

2)

|x-1|-x>|x+2|+x-3

x-1 \geq 0 \iff x\geq 1

x+2 \geq 0 \iff x\geq -2

Per cui avremo:

\begin{cases} x \leq -2 \\ 1-x-x>-x-2+x-3 \end{cases} \quad \quad \begin{cases} -2<x<1 \\ 1-x-x>x+2+x-3 \end{cases}\quad \quad \begin{cases} x\geq 1 \\ x-1-x>x+2+x-3 \end{cases}

\begin{cases} x \leq -2 \\ 1-2x>-5 \end{cases} \quad \quad \begin{cases} -2<x<1 \\ 1-2x>2x-1 \end{cases}\quad \quad \begin{cases} x\geq 1 \\ -1>2x-1 \end{cases}

\begin{cases} x \leq -2 \\ x<3 \end{cases} \quad \quad \begin{cases} -2<x<1 \\ x<\frac 12 \end{cases}\quad \quad \begin{cases} x\geq 1 \\ x<0 \end{cases}

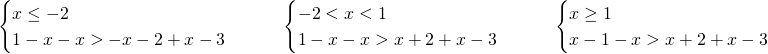
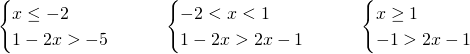
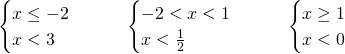
Per cui:

il primo sistema avrà come soluzione x \leq -2

il secondo sistema avrà come soluzione -2<x < \frac 12

Il terzo sistema non ammette soluzione.

Unendo le tre avremo la soluzione della disequazione:

x<-\frac 12

(Questa pagina è stata visualizzata da 57 persone)

Lascia un commento