Emanuele scrive: Studio di una funzione

Pubblicato il da Lo StaffLascia un commento
0

Oggetto: Studio di una funzione

Corpo del messaggio:
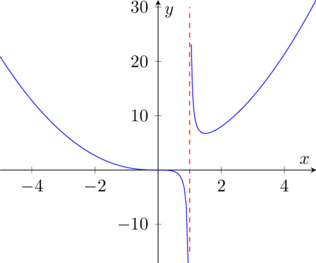
Studiare e graficare la seguente funzione: y= x^3 / x-1

Vi chiedo un favore se potevate essere rapidi che domani ho l’esame di riparazione grazie mille!!

image-23

 

Risposta dello staff

y=\frac{x^3}{x-1}

Dominio:

x-1 \neq 0

x \neq 1

D: ] -\infty; 1 [ \, \, \cup \, \, ]1;+\infty[

Studiamo la positività:

f(x) \geq 0

\frac{x^3}{x-1}\geq 0

N \geq 0 \iff x \geq 0

D>0 \iff x >1

Per cui:

f(x) >0 \iff x <0 \quad \lor \quad x>1

f(x) =0 \iff x =0

f(x) <0 \iff 0<x <1

Verifichiamo eventuale parità o disparità:

f(x)=\frac{x^3}{x-1}

f(-x)=\frac{x^3}{x+1}

-f(x)=\frac{x^3}{1-x}

Non avrà simmetrie.

Studiamo i limiti negli estremi del dominio:

    \[\lim_{x \to \pm \infty} f(x)= +\infty\]

    \[\lim_{x \to 1^-} f(x)= -\infty\]

    \[\lim_{x \to 1^+} f(x)= +\infty\]

Essendo la differenza di grado tra numeratore e denominatore maggiore di 1, non ci sarà asintoto obliquo.

Studiamo ora la crescenza e la decrescenza:

f'(x)=\frac{3x^2(x-1) - x^3}{(x-1)^2}

f'(x)=\frac{3x^3-3x^2 - x^3}{(x-1)^2}

f'(x)=\frac{2x^3-3x^2 }{(x-1)^2}

f'(x)=\frac{x^2(2x-3) }{(x-1)^2}

Per cui, avremo che:

N_1: x^2 \geq 0 \forall x \in \mathbb{R}

N_2: 2x-3 \geq 0 x \geq \frac 32

D: (x-1)^2 > 0 \forall x \in \mathbb{D}

f'(x) >0 \iff x > \frac 32

f'(x) =0 \iff x = \frac 32 \quad \lor \quad x=0

f'(x) <0 \iff x<0 \quad \lor \quad 0<x < 1 \quad \lor \quad 1<x<\frac 32

x=\frac 32 è punto di minimo.

Studiamo la derivata seconda:

f''(x)=\frac{(6x^2-6x)(x-1)^2-(2x^3-3x^2)2(x-1)}{(x-1)^4}

f''(x)=\frac{(6x^2-6x)(x-1)-4x^3+6x^2}{(x-1)^3}

f''(x)=\frac{6x^3-6x^2-6x^2+6x-4x^3+6x^2}{(x-1)^3}

f''(x)=\frac{2x^3-6x^2+6x}{(x-1)^3}

f''(x)=\frac{2x(x^2-3x+3)}{(x-1)^3}

Essendo x^2-3x+3>0 per ogni x, avremo:

f''(x)>0 \iff x<0 \quad \lor \quad x>1

f''(x)=0 \iff x=0

f''(x)<0 \iff 0<x<1

Rendered by QuickLaTeX.com

 

(Questa pagina è stata visualizzata da 47 persone)

Lascia un commento