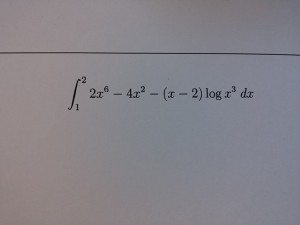Fabio scrive: procedimento integrale

Oggetto: procedimento integrale

Corpo del messaggio:

$\int_1^2 2x^6-4x^2-(x-2)logx^3 \, dx$

Risolviamo i primi 2 fattori che sono integrali immediati:

$\int_1^2 2x^6 \, dx=\left[ \frac 27x^7\right]_1^2=\frac{256-2}{7}=\frac{254}{7}$

$\int_1^2 4x^2 \, dx=\left[ \frac 43x^3\right]_1^2=\frac{32-4}{3}=\frac{28}{3}$

Per l’ultimo pezzo integriamo per parti:

$3\int (2-x)logx \, dx$

$f(x)=log x \rightarrow f'(x)=\frac 1x$

$g'(x)= 2- x \rightarrow g(x)=2x-\frac 12 x^2$

L’integrale diventa quindi:

$3logx(2x-\frac 12 x^2)-3\int \frac{2x-\frac 12 x^2}{x} \, dx=$

$3logx(2x-\frac 12 x^2)-3\int (2-\frac 12 x) \, dx=$

$3logx(2x-\frac 12 x^2)-3(2x-\frac 14 x^2)+C$

Calcoliamolo tra 1 e 2 e otteniamo:

$3\int_1^2 (2-x)logx \, dx=3[logx(2x-\frac 12 x^2)-2x+\frac 14 x^2]_1^2=3(2log2-3+2-\frac 14)=3(2log2-\frac 54)$

Mettendo tutto insieme avremo:

$\int_1^2 2x^6-4x^2-(x-2)logx^3 \, dx=\frac{254}{7}-\frac{28}{3}+ 3(2log2-\frac 54)$

(Questa pagina è stata visualizzata da 53 persone)

Matebook