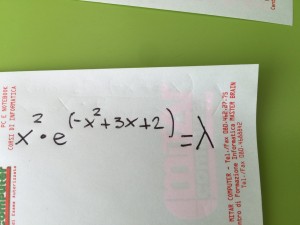Determinare al variare di lambda il numero delle soluzioni
Risposta dello staff
Studiamo la funzione ![]()
Il dominio sarà tutto ![]() essendo
essendo ![]() definita in tutto
definita in tutto ![]() e l’esponente una funzione polinomiale.
e l’esponente una funzione polinomiale.
La funzione essendo formata da un prodotto di ![]() e una funzione esponenziale, sarà sempre positiva, e si annullerà solo per
e una funzione esponenziale, sarà sempre positiva, e si annullerà solo per ![]()
Quindi avremo:
![]()
![]()
![]() .
.
Studiamo i limiti negli estremi del dominio:
![]()
In quanto l’esponenziale all’infinito è di ordine superiore.
Studiamo la derivata prima:
![]()
![]()
![]()
Studiamo la positività della derivata prima:
![]()
![]()
![]()
![]()
![]()
![]()
Per cui:
![]()
Quindi, facendo il grafico delle soluzioni (non so disegnarlo qui), avremo che:
f crescente per ![]()
![]() punto di massimo con
punto di massimo con ![]()
f decrescente per ![]()
![]() punto di minimo con
punto di minimo con ![]()
f crescente per ![]()
![]() punto di massimo con
punto di massimo con ![]()
f decrescente per ![]()
Infine possiamo capire, tracciando il grafico, il numero di soluzioni al variare di ![]() :
:
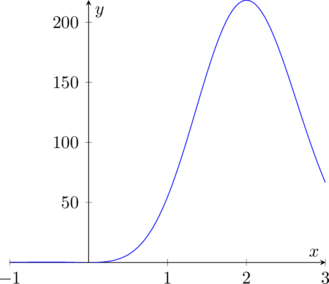
![]() non avrà soluzione.
non avrà soluzione.
![]() 1 soluzione.
1 soluzione.
![]() 4 soluzioni.
4 soluzioni.
![]() 3 soluzioni.
3 soluzioni.
![]() 2 soluzioni.
2 soluzioni.
![]() 1 soluzioni.
1 soluzioni.
![]() nessuna soluzione.
nessuna soluzione.
(Questa pagina è stata visualizzata da 41 persone)