Francesca scrive: Risoluzione della funzione

Pubblicato il 30 Settembre 2015 da Lo StaffLascia un commento

Oggetto: Risoluzione della funzione

Corpo del messaggio:

$y=x^4-4x^2$

Risposta dello staff

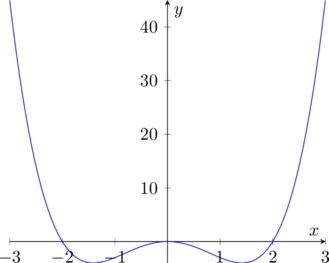
Essendo una funzione razionale intera il dominio è tutto $\mathbb{R}$ . Studiamo la positività:

$x^4-4x^2>0$

$x^2(x^2-4)>0$

$x^2>0 \qquad \forall x - \{0\}$

$x^2-4>0 \iff -2<x<0 \quad \lor \quad 0<x<2$

Quindi avremo che:

$f(x)>0 \iff x<-2 \quad \lor \quad x>2$

$f(x)=0 \iff x=\pm 2 \quad \wedge \quad x=0$

$f(x)<0 \iff -2<x<2$

E’ una funzione pari, in quanto $f(x)=f(-x)$ .

Studiamo i limiti agli estremi del dominio:

$\lim_{x \to \pm \infty} f(x)=+ \infty$

Studiamo la derivata prima:

$f'(x)=4x^3-8x$

Studiamo la positività della derivata prima:

$4x^3-8x>0$

$4x(x^2-2)>0$

$4x>0 \iff x>0$

$x^2-2>0 \iff x<-\sqrt 2 \quad \lor \quad x> \sqrt 2$

Quindi:

$f'(x)>0 \iff -\sqrt 2<x<0 \quad \lor \quad x>\sqrt 2$

$f'(x)=0 \iff x=\pm \sqrt 2 \quad \wedge \quad x=0$

$f'(x)<0 \iff x<-\sqrt 2 \quad \lor \quad 0<x<\sqrt 2$

Studiamo la derivata seconda:

$f''(x)=12x^2-8$

Studiamo la positività:

$12x^2-8>0$

$3x^2-2>0$

$x^2>\frac 23$

$x< -\sqrt{\frac 23} \quad \lor \quad x>-\sqrt{\frac 23}$

Rendered by QuickLaTeX.com

(Questa pagina è stata visualizzata da 50 persone)

Lascia un commento Annulla risposta