Oggetto: Problema spazio vettoriale

Corpo del messaggio:
Buongiorno, ormai è da varie ore che sto cercando di risolvere questo esercizio ma non trovo nessuna soluzione.
L’esercizio è il seguente : Siano u , v , w tre vettori linearmente indipendenti in uno spazio vettoriale reale V . Provare che  per ogni scelta di a,b,c e(appartentente ) R i vettori u, v+av , w+bu+cv sono ancora linearmente indipendenti .

io so dalla teoria  che per essere linearmente indipendenti essi devono essere uguali a 0 solo per valori tutti nulli , ma qui non so proprio come dimostrarlo . Grazie in anticipo

Risposta dello staff

Basterà calcolare il determinante della matrice dei coefficienti:

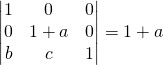
Quindi, per avresti rango 2.

Per i vettori sono linearmente indipendenti.

 

(Questa pagina è stata visualizzata da 35 persone)