Esercizio 17 Equazioni parametriche

-5

Traccia

Determinare per quali valori di k la somma delle soluzioni reali dell’equazione (4-k^2)x^2+2kx+1-k^2=0 è maggiore di 3.

Svolgimento

Dobbiamo studiare per quali valori di k  è possibile calcolare le radici.

(4-k^2)x^2+2kx+1-k^2=0

Per capire per quali valori di k l’equazione avrà soluzioni reali, basterà semplicemente studiare la positività del \Delta.

a=4-k^2

b=2k

c=1-k^2

\Delta=4k^2-4(4-k^2)(1-k^2)

\Delta=4k^2-16+16k^2+4k^2-4k^4

\Delta=-4k^4+24k^2-16

Imponiamo ora che \Delta \geq 0 e avremo:

-4(k^4-6k^2+4) \geq 0

4(k^4-6k^2+4) \leq 0

L’equazione associata ammetterà come soluzioni,

k^2_1= 3 - \sqrt {5} \quad \wedge \quad k^2_2=3+\sqrt 5

il che implica che, andando a vedere la tabella delle disequazioni, il risultato sarà:

3-\sqrt 5 \leq k^2 \leq 3+\sqrt 5.

Quindi questa sarà:

\begin {cases} k^2 \geq 3-\sqrt 5 \\ k^2 \leq 3+\sqrt 5 \end {cases}

\begin {cases} k \leq - \sqrt {3-\sqrt 5} \quad \lor \quad k \geq \sqrt{3+\sqrt 5} \\ -\sqrt{3+\sqrt5} \leq k \leq +\sqrt{3+\sqrt 5} \end {cases}

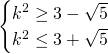
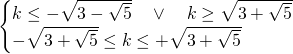
Affinchè si verifichi che la somma delle soluzioni sia maggiore di 3, deve accadere che:

-\frac b a >3

-\frac {2k}{4-k^2} >3

\frac {-2k}{4-k^2}-3>0

\frac {-2k-12+3k^2}{4-k^2}>0

\frac {3k^2-2k-12}{4-k^2}>0

  • N>0

3k^2+2k-12 >0

k_{\frac 12}=\frac {2 \pm \sqrt {4+144}}{6}=\frac {2 \pm 2\sqrt {37}}{6}=\frac {1 \pm \sqrt{37}}{3}

k< \frac {1-\sqrt{37}}{3} \quad \lor \quad k> \frac {1+\sqrt{37}}{3}

  • D>0

4-k^2>0

k^2-4<0

-2<k<2.

Analizzando entrambe le soluzioni, la frazione sarà verificata per:

-2<x<\frac {1-\sqrt{37}}{3} \quad \lor \quad 2<x<\frac {1+\sqrt{37}}{3}.

Intersecando queste soluzioni con la possibilità di avere radici reali, la soluzione cambia leggermente poichè i valori sono leggermente diversi, e la soluzione finale sarà:

-2<x<\frac {1-\sqrt{37}}{3} \quad \lor \quad 2<x<\sqrt{3+\sqrt 5}.

 

 

 

Altri esercizi simili

 

 

(Questa pagina è stata visualizzata da 515 persone)

Lascia un commento