Enunciato
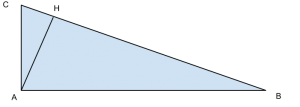
Sia ABC un triangolo rettangolo retto in A, e sia AH l’altezza relativa all’ipotenusa.
Chiameremo CH e HB le proiezioni rispettivamente dei cateti AC e AB.
Ogni teorema lo si può vedere rappresentato in due modi: come uguaglianza di figure oppure come relazione tra segmenti.
Primo Teorema di Euclide:
– In un triangolo rettangolo, il quadrato costruito su un cateto è equivalente al rettangolo che abbia per dimensioni l’ipotenusa e la proiezione del cateto stesso.
![]()
![]() .
.
– In un triangolo rettangolo, il cateto è medio proporzionale tra l’ipotenusa e la sua proiezione sull’ipotenusa:
![]()
![]()
Secondo teorema di Euclide:
– In un triangolo rettangolo, il quadrato costruito sull’altezza è equivalente al rettangolo che abbia per dimensioni le proiezione dei due cateti sull’ipotenusa stessa.
![]() .
.
– In un triangolo rettangolo, l’altezza relativa all’ipotenusa è media proporzionale tra le due proiezioni dei due cateti sull’ipotenusa stessa:
![]()
Esercizi sul teorema di Euclide
Altri hanno visualizzato anche:
(Questa pagina è stata visualizzata da 593 persone)
E bellissimo utilissimo domani ho il compito di matematica . sono sicura che riuscirò a prendere un bel voto grazie a voi…..