Uno studente scrive:
Oggetto: Problema
Corpo del messaggio:
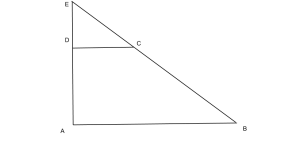
In un trapezio rettangolo ABCD l’ altezza AD è i 3/2 della base minore CD che, a sua volta, è i 4/9 della base maggiore AB. La somma delle due basi è 52k. Prolungando l’ altezza ed il lato obliquo, i due prolungamenti si intersecano nel punto E. Calcola l’ area del triangolo ABE.
Risposta dello staff
Chiamiamo ![]() , così da avere, rispetto ai dati
, così da avere, rispetto ai dati
![]()
![]()
Dalla somma delle basi otteniamo il valore dell’incognita:
![]()
![]()
![]()
![]()
Quindi:
![]()
![]()
Usando la regola delle proporzioni otteniamo DE (![]() ) sui triangoli DEC e ABE:
) sui triangoli DEC e ABE:
![]()
![]()
![]()
![]()
![]()
![]()
Quindi l’area del triangolo sarà:
![]()
(Questa pagina è stata visualizzata da 290 persone)