Maria scrive: Esercizio triangolo rettangolo

Pubblicato il da Lo StaffLascia un commento
0

Uno studente scrive:

Oggetto: Problemi con similitudini

Corpo del messaggio:

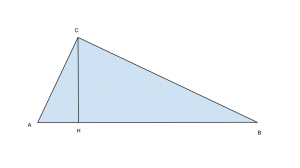
1) In un triangolo rettangolo, l’ altezza relativa all’ ipotenusa è lunga a e la proiezione del cateto maggiore sull’ ipotenusa supera di 2a\sqrt{ 3} la proiezione del cateto minore. Calcola il rapporto fra le aree dei triangoli rettangoli che l’ altezza determina.

 

Risposta dello staff

triangolorettangoloaltezza

 

Dai dati sappiamo che:

CH=a

BH=AH+2a\sqrt {3}

Dal teorema di Euclide otteniamo subito:

AH \cdot HB=CH^2

Chiamando AH=x per comodità otteniamo:

x (x+2a\sqrt{3})=a^2

x^2+2ax\sqrt{3}-a^2=0

x_{\frac 12}=\frac {-2a\sqrt{3} \pm \sqrt {12a^2+4a^2}}{2}

x_{\frac 12}=\frac {-2a\sqrt{3} \pm \sqrt {16a^2}}{2}

x_{\frac 12}=\frac {-2a\sqrt{3} \pm 4a}{2}

x_{\frac 12}=-a\sqrt{3} \pm 2a

Ovviamente avrà una sola soluzione accettabile:

x=2a-a\sqrt{3}

quindi:

AH=2a-a\sqrt{3}

BH=2a+a\sqrt{3}

Ora possiamo calcolare i rapporti delle due aree:

\frac {A_{CBH}}{A_{ACH}}=\frac {\frac {BH \cdot CH}{2}}{\frac {AH \cdot CH}{2}}=\frac {BH}{AH}

\frac {A_{CBH}}{A_{ACH}}=\frac {2a+a\sqrt 3}{2a-a\sqrt 3}=\frac {2+\sqrt 3}{2-\sqrt 3}=\frac {2+\sqrt 3}{2-\sqrt 3} \cdot \frac {2+\sqrt 3}{2 + \sqrt 3}=\frac {(2+\sqrt 3)^2}{4-a}=4+4\sqrt 3 +3=7+4\sqrt 3

 

 

(Questa pagina è stata visualizzata da 161 persone)

Lascia un commento