Una studentessa scrive:
Oggetto: problema con equazione
Corpo del messaggio:
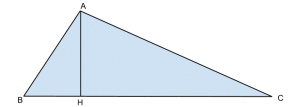
in un triangolo rettangolo ABC la somma del cateto minore AB e l’ipotenusa BC è 48 m, il cateto AC è 24 m. calcola le misure dei due lati incogniti e l’area
Risposta dello staff
Dai dati abbiamo che:
![]()
![]()
Ponendo ![]() , otteniamo:
, otteniamo:
![]()
e sfruttando il teorema di Pitagora otteniamo:
![]()
![]()
![]()
![]()
![]()
Quindi:
![]()
![]()
L’area sarà uguale al semiprodotto dei cateti:
![]() .
.
(Questa pagina è stata visualizzata da 121 persone)